Not a blackhat. Not a whitehat. A clearhat.
Neither left nor right but decidedly in the center
Version 1.3
Clearhat as an idea is a thought-provoker, a challenge to the ordinary which reflects back like a mirror to reveal unexpected meaning hidden in plain sight within the ordinary.

The clearhat concept has something to do with realizing there is an endless war between blackhats and whitehats that has been going on for centuries, even millennia, perhaps since the dawn of civilization itself: For every whitehat that appears on the scene, there is a blackhat out there, who is or soon becomes an equal. They create each other; as one develops a new skill, the other learns how to oppose or overcome that skill, and vice-versa. It's like an arms race, where each battle is won by the side that develops the best new weapon, but the war itself never ends.
So the clearhat way is for someone who sees this, looks beyond good and evil, and realizes: "No matter how good I am, no matter how bad I am, no matter how skilled I am, nor how poor I am; whether I succeed or whether I fail, I'm contributing to an endless war between two opposing forces, which existed before I was born, and will exist long after I'm gone."
The clearhat, then, aims at a different target than "one side, or the other," and engages in a third game -- neither wholly white nor black, but what turns out to be the substratum upon which both exist.
And no, this denial of extremes does not mean greyhat, or redhat, or really anything with color. With clear as a color, color as a category itself gets transcended, since clear is obviously not a color.
Nevertheless this is not just a paradox you can discard because it is nonsensical: It turns out, interpreting clear as a color turns out to be a meaningful metaphor. This is because it is immediately "clear" to someone who starts thinking of clear as a color that there is something right in front of them -- everywhere, actually -- which has always been there, which they have never seen before.
To a few, who are weary of the over-polarized world, this is an open door into another way of thinking about... everything.
In times like these, it's dangerous to be neutral
 At first glance, the seeming neutrality of the clearhat position appears weak. If any strength is seen in it, the strength is seen by others as a betrayal because there is an implicit "if you're not for us, you're against us" embedded in the way people see the world.
At first glance, the seeming neutrality of the clearhat position appears weak. If any strength is seen in it, the strength is seen by others as a betrayal because there is an implicit "if you're not for us, you're against us" embedded in the way people see the world.
Even though children are not like this, such polarization happens globally as people become adults. It happens even in the East, although it does have a stronger non-binary cultural awareness than the West. We live in a world which is polarized, on so many levels.
At the kindest end of the polarized view, the clearhat perspective is "indecisive," "incompetent," or "immature," like a hesitant "maybe" in a garden of firm "yeses" and "nos."
At the unkind end, the clearhat role is that of a "liar," a "spy," a "traitor," even though it is none of these.
The essential point being made here is both ends think that the middle is inferior in one way or another. However, think about things for a moment and you will see: these adjectives are all projected labels. The polarity is embedded in the way people see, not in what actually is.
As hinted earlier, this projection happens invisibly because there is an implicit polarity embedded throughout our culture. There is little tolerance for people in the middle who can't make up their minds, especially when there's a war going onTM.
In short, xenophobia runs deep in the herd mentality in which we all play a role. This makes it dangerous to sit in the middle of any polarity and politely refuse to be aligned with either side.
For this reason, one with the clearhat view strives to be morally and ethically... hmmm... not "good," per se, but... unexceptional. Or ordinary. Neither saintly nor demonly -- because these draw attention and polarize -- but ordinary.
Ordinary is what's in the middle of extremes like hero vs scapegoat
Although unintentional ordinariness happens to everyone without thought, the challenge to be intentionally ordinary can be difficult, because in a way it is a counter-projection from the realm of self-awareness. This approach, because of self-awareness, demands more honesty than is required from the extremes. Here's why: 1. The extremist can can hide their flaws behind projected "white" or "black" labels. 2. Everyone on "their" side will agree without looking more closely. 3. Any attacks from the "other" side are easily deflected as being against the group, not the individual.
This leaves a gap where neither introspection nor other-inspection function in pure form, because they are biased by group dynamics.
For this reason, intentional ordinariness is not shareable; it is an individual journey, because talking about how to be ordinary is not something ordinary people do. For the ordinary person, being ordinary happens without thought, but for the extraordinary, being ordinary requires thought, and is not so easy. It requires intention and incremental behavior modification over a long period of time.
Over time, it becomes clear: the art of simply "being ordinary" cultivates a process of continual improvement in a Zen-like manner. What is forged by the process is a flavor of humbleness which is neither weak nor subservient. It is consciously self-limiting in a way which is difficult for the extraordinary mind to do. But it turns out, putting effort into this makes everything more efficient, because a hidden simplicity, an unadorned honesty, begins to appear. This internal pressure driving toward honesty transcends "sides." It is therefore more principled than ordinary honesty. The ideas behind radical honesty are relevant here, but in a... moderate, practical, non-polarizing, manner.
But wait: not too non-polarizing. This is not about passivity. Being passive-aggressive or many other ways of seeming to be one thing while being another is only one of the character flaws which the clearhat position must methodically overcome as soon as its underlying deception becomes visible: While passivity seems to require little energy, this is not always the case. Indeed, on close study, passivity is a condition hiding a cumulative tension going on behind the scenes which eventually requires expending enormous energy in order to maintain the status quo within which such passivity can exist.
 This is an elusive idea, so let's break it down a little more: The quiet betrayal of the passive-aggressive may seem gentler than the obvious anger of the overtly aggressive, but in fact it's equally damaging. They both expose an underlying deception, although one is harder to discern in a short frame.
This is an elusive idea, so let's break it down a little more: The quiet betrayal of the passive-aggressive may seem gentler than the obvious anger of the overtly aggressive, but in fact it's equally damaging. They both expose an underlying deception, although one is harder to discern in a short frame.
Studied over a span of time, it becomes clear: the passive-aggressive person must play the role of hero at times, but not because he is a hero. Rather he does this solely to cover up the truth of his underlying weaknesses -- which is a villain motive, not a true hero motive.
A hero role requires energy, sometimes quite a lot. The physics of being intentionally ordinary reveals that the "occasional enormous energy" plus the "usual lower energy" of the passive-aggressive type requires more overall effort than simply being consistent at all times, a point which Mark Twain observed when he wrote in a notebook in 1894: "If you tell the truth you don't have to remember anything."
Self-awareness as a means to simplicity
In the interest of simplicity, then, a kind of thoughtful asceticism develops within a clearhat mind: self-awareness as a means to simplicity, rather than self-awareness as an end, which is taught by the meditators.
Like driving a car in the rain, where oversteering can have immediate and extreme consequences, the clearhat role of being two things simultaneously -- while also being honest -- is hard work. Thus there is a sincere appeal toward the elegance of Twain's personal integrity implied by the clearhat label. On the surface, this aligns integrity with the clearhat label, but under the hood the motive is quite different from the whitehat, who outwardly claims integrity.
The whitehat is achieving an outward veneer of integrity according to an external standard, whereas the clearhat is achieving the most elegant path according to an inward standard. The view from the clearhat role sees that whitehats -- and they themselves -- often pretend or even fool themselves or others that they have such inner integrity, but in truth, many so-called whitehat actions are about outward virtue-signaling: a means to cover up their "inner blackhat" as illustrated in the hero example above.
The clearhat is abandoning such covering-up and learning to see character flaws as statements about the human condition, rather than as statements about personal culpability. Their labor is about bringing humanity upward, not about one individual or another, but everyone. This paradigm shift leaves them striking at the root of the tree of evil instead of merely trimming at the leaves. Letting go of the need to be seen outwardly as virtuous paradoxically makes achieving true virtue a more powerful, shared, journey. This is a win for the end game of simplicity.
Calling oneself a clearhat is a way of misunderstanding the essential point about simplicity here: one can adopt a clearhat view and learn from it, but one can never "be" a clearhat because that would be like the color blue "being" clear. If you want to "be" clear, you must stop being whatever else you are. This is not a paradox, it is a boundary. If you claim to be a clearhat, you have at least one more step of simplification to go. See the logical flaw of "is" below for more on this point.
The clearhat approach takes time and is a process, not a state
The clearhat model is not a standard born in a day; it takes years to achieve these goals, working slowly and steadily toward them while the vicissitudes of a normal life play through on their daily cycles. A clearhat path arises out of a lot of chaos which takes time to resolve, and a lot of time it looks like it's an impossible goal.
One who dons the clear hat does not like so-called whitehats any more than they like blackhats.  Their heroes are found on both sides because the metric is not about external appearances, but more about inner integrity and the narrative which makes people grow. So of course, they like both, but carefully.
Their heroes are found on both sides because the metric is not about external appearances, but more about inner integrity and the narrative which makes people grow. So of course, they like both, but carefully.
It turns out, most of the day-to-day problems the clearhat approach encounters come from whitehats who are self-righteous and thus unable to see their own character flaws and therefore project them on to other people without realizing what they're doing.
Anyone with a clear hat becomes an easy target for such projection, for the reasons explained above. Thus, the clearhat role aims for a lifestyle resilient to such tactics and wise to the whitehat flaws -- as well as the more obvious blackhat ones which everyone knows.
Inwardly, the clearhat model is for one who invents a path forward which is somehow both and neither, together, simultaneously, choosing to do those things "against which there is no law," walking in that forbidden land between giants who throw stones at each other every day (see illustration, borrowed from the Narnia adventures).
Their game is about things like structural clarity, simplicity, and elegance, not win vs. lose. Beauty, not victory, because beauty is the victory. The long arc of means tends toward the end of beauty only if beauty is woven in to the means all along.
The logical flaw of "is" goes deep
The age-old black-white struggle may seem structurally simple because it only has two elements, but upon analysis, it describes an incredibly complex global game with many layers of redirection hiding an inherent logical weakness that, like the emperor's new clothes, few can see and no one dares admit.
This hiding aspect is what makes its seeming simplicity so complicated. The logical weakness has to do with the map-territory confusion as observed by Alfred Korzybski a century ago (1931): We tend to identify concrete things with their abstracted form, and then relate to the concrete form as if it were the abstract.
An example is a preacher who believes that because he is a preacher, he is a good person, and therefore puts little effort to improve his internal personal character, because... why? He is already good. He has confused who he is with the abstraction that others assign to his role. This is a logical fallacy. (In this example, we're ignoring the effort required to appear to be doing such internal character development, which is part of the role of being "good," because that is entirely about appearances. We're also ignoring his daily self-doubt, which everyone has. We're looking deeper into what is, not simply what appears.)
The sad part of this example is that he is surrounded by people who reinforce him doing this: Because they need someone to look up to, they believe that he is good, overlook his flaws, and relate to him as if he were the abstract, good, form he projects himself to be.
The preacher is just an example. In fact, we all do this; we all live in "the map" and lose touch with "the territory" which is the truth of who we really are. In the story of Adam and Eve, placing the fig leaf to cover nakedness started the separation between map and territory. The gap between these two is the logical fallacy. The problem here is not in the existence of the map. It is in how the map is deeply polarized, while the territory is not. In other words, the "map" of racism is different than the "territory" of race, and in all the noise about the former, the intricate beauty of the latter goes unexplored. This is true of all the isms.
The black and white map is not the clearhat territory
Likewise, the polarized map has no place for the clearhat position, although the territory does. In its article on Alfred Korzybski, Wikipedia does a decent job of summarizing the crux of the problem and how it relates to the word "is":
...certain uses of the verb "to be", called the "is of identity" and the "is of predication", were faulty in structure, e.g., a statement such as, "Elizabeth is a fool" (said of a person named "Elizabeth" who has done something that we regard as foolish). In Korzybski's system, one's assessment of Elizabeth belongs to a higher order of abstraction than Elizabeth herself. Korzybski's remedy was to deny identity; in this example, to be aware continually that "Elizabeth" is not what we call her. We find Elizabeth not in the verbal domain, the world of words, but the nonverbal domain (the two, he said, amount to different orders of abstraction). This was expressed by Korzybski's most famous premise, "the map is not the territory". (Wikipedia)
 Although the logical flaw of the map seems to be a cultural phenomenon (as noted above, most obvious in the West), it is actually rooted in biology. In sociobiological terms, it's part of the way herd animals operate, but it actually goes deeper than that.
Although the logical flaw of the map seems to be a cultural phenomenon (as noted above, most obvious in the West), it is actually rooted in biology. In sociobiological terms, it's part of the way herd animals operate, but it actually goes deeper than that.
At a hardware level, it is an artefact of a left-brain way of seeing things that is out of balance with the right brain. See the Iaian McGilchrist quote to the left for more on how this works. The story of this imbalance reaches all the way back into evolution's grand struggle for survival.
Neither a hawk nor a dove, but able to be either if the need arises
The differences between these two realms are related to the great maxim of sociobiology: "Selfishness beats altruism within groups. Altruistic groups beat selfish groups."
A person is continually moving between these two zones of altruistic and selfish identity, and optimally should be balanced between the two, able to play a role in either realm at will as conscience dictates.
As McGilchrist points out elsewhere, as a culture we're much too far into the selfish left brain way of seeing, and need to come back to the middle. The clearhat way does this by stepping out of the polarizing game.
Instead of inventing the next great weapon, or its antidote, the clearhat approach is inventing clever, simple, ways to get by without weapons altogether.
Does this mean the clearhat model is pacifist? No; there are times when the pacifist is the traitor, and the clearhat role -- sometimes accused of such things by simply being neither here nor there, is especially sensitive to this point.
The clearhat approach aims to pursue happiness, as the Declaration of Independence succinctly put it long ago. In this vein, unlike extreme pacifism, the clearhat sees that weapons may be appropriate at times -- as they were when that document was written, and as they inevitably are when they are taken away en masse. However, if so, they are seen as temporarily so, not to be carried on the hip forever, but only until certain existential threats pass. For example, the right to bear arms is not a commandment to bear arms, it's just a right that should never be infringed because history shows what a mess we get into when it is infringed. Bear arms or do not as you will, but never mess with the right to do so because no matter how horrible things may be, they always get worse when that right is abridged.
The temporary aspect here is important -- black or white thinking likes to project things with an implied absolutivity, when reality itself has few absolutes and carries plenty of flexibility, degrees of freedom, transience. For example, think about how many people you know who prefer to carry weapons. Do any of them do so temporarily? More likely, they have made life-long commitments to this belief system, such as seen in "you can have it when you pry it from my cold, dead hands."
Like cats with retractable claws -- there when you need them, otherwise not -- the clearhat model encourages thinking deeply about such things. The clearhat approach seeks to understand when it is appropriate to make such a commitment, and when it is appropriate to let go. It draws attention to the simpler joys which are invisible to those who are always in Defense Mode. This seeming "inconsistency" may seem complicated to people who adhere to the absolutist version of simplicity, but in fact, it is a simpler way in practice, allowing more degrees of freedom. If the context changes, the clearhat model adapts; other models stay rigid. But adapt too much and... you've left the simplicity of the clearhat model.
Clearhat simplicity must be a liveable one, not fake or academic, idealistic, theoretical, or extreme. Those are all fragments of zero-sum pursuits, and we're talking about something more coherent, more holistic. However, this is not about going into the desert and living like a monk, in a vacuum adhering to a few narrow principles by eliminating many practical challenges. This is about living in the midst of a polarized culture, blending in, being ordinary, joining the ordo ordinarium -- the order of the ordinary people -- being one with the common man. Here, in ordinariness, is where the idealistic extremes of polarized cultures are able to fall away in favor of the simple and ordinary things which comprise the daily life of the simple and ordinary.
What's unique about clearhat? If it's about simplicity, why not simply align with other "middle way" approaches?
The unusual approach being discussed here is a little more sophisticated than it may seem on the surface. It is rooted in a decades-deep study of trinary logic[1] or "non-linear logic" which consistently turns up unique insights not found in any previous implementation of logic, including trinary/ternary itself. This website, clearhat.org, is an exploration of those insights. This narrative on the front page is just one way of organizing some of them which have evolved over time and will continue to do so as these thoughts mature.
The rest of this website is another way of delivering these ideas. It follows a roughly chronological evolution of thought that reaches back into the 1990s. This so-called "clearhat" version was started around 2009. Due to the journal style of publishing and a peripatetic style of learning, such thoughts are sometimes interspersed with unrelated information more appropriate for a blog run by a software engineer. This interleaving actually catches an important point about the clearhat approach: it is lived, not simply believed, and it is intended to be woven in with other approaches in the same manner the ordinary is found mingled with the extraordinary.
There are other non-duality websites out there, in fact, many. Buddhism, Zen, and other practices reveal robust and ancient ways to be something that is effectively the same as clearhat. There is plenty of overlap between these ways of being, but on close inspection, the resemblance to clearhat is often superficial. There are nuances which make a world of difference. Maybe it's the "lifestyle as a method of study" approach, which means that the clearhat perspective studies the world not only intellectually, but by living what is believed, watching carefully what happens as beliefs change over time because they're intersecting with reality -- not just other beliefs or a vacuum -- and then using the new information to guide further study. Maybe it's the emphasis on logic and mathematics, an approach which draws different things to the surface than you find in religion and philosophy alone. There's a certain rigor in these fields which tends to straighten out misconceptions over time.
Case study: The Middle Way Society is not as non-binary as it aims to be
 For example, The Middle Way Society seems on the surface to be saying much the same things about non-binary as you find here. It appears to be a nicely mature perspective; the author has written multiple books and has extensive online material. Even better, the site is heartily endorsed by Iain McGilchrist (quoted above), one of the world's leading experts on non-binary thought structures and how they relate to linear, binary ones.
For example, The Middle Way Society seems on the surface to be saying much the same things about non-binary as you find here. It appears to be a nicely mature perspective; the author has written multiple books and has extensive online material. Even better, the site is heartily endorsed by Iain McGilchrist (quoted above), one of the world's leading experts on non-binary thought structures and how they relate to linear, binary ones.
But a closer look at the Middle Way Society reveals that the author of this particular way is actually using a binary approach to non-binary. At the core of their solution is a denial of absolutes -- both positive and negative. This denial is presented as the method for choosing "the middle way" between the two extremes.
This seems quite logical, but it is not the clearhat way. It is logical in a way that depends on and reinforces the Law of Excluded Middle instead of seeing the true trinary Included-Middle which exists beneath it as a foundation.
Here's how: in order to "deny absolutes," you must establish a new absolute forged from denial. This new absolute is in opposition to both existing poles -- which are already in opposition to each other.
Adding opposition to opposition cannot be a way of peace, as it is hoped. In fact, it ironically does the exact opposite of what it intends to be doing, adding fuel to a fire instead of adding water.
This kind of approach sounds great, and works for awhile, years, decades, even centuries... but with continually diminishing returns until all observed absolute-pairs have been successively denied, and then it begins eating itself, because there is nothing left to oppose. Evidence that this happens became clear in a number of failed thought experiments early in the clearhat journey, and was finally rejected well before this website began.
This is not how to find a middle way; it's how to find nihilism: "How to hate everyone while appearing nice and still think you're right." It looks good on the surface but underneath it is not built on a solid foundation.
Looking under the hood even more: the true "middle way" sees the binary nature of opposition itself
The problem here is a misunderstanding about the binary nature of opposition itself. To create an absolute which denies absolutes is seen as a logical absurdity within trinary logic, although it is perfectly reasonable within binary logic pretending to be non-binary where it's simply another casual implementation of the Law of Excluded Middle.
Trinary logic excludes nothing, or rather, to say it more coherently: trinary logic includes everything. Even things which oppose it. It is not like a sword conquering opposition by dividing asunder, it is more like a sphere growing and encompassing opposition into itself. "Be like water, my friend," is how Bruce Lee famously put it once, talking about how water takes the shape of the container rather than imposing itself upon the world.
During the long study of trinary logic mentioned above, this superficial structure (denying absolutes) represented an early stage of inquiry which eventually proved to be as just described: a binary way of approaching non-binariness. A house divided against itself, built on sand. This denial of absolutes does not solve the problem of opposite absolutes, but extends it by introducing a new absolute which opposes all others and injects itself in their place. Do you recognize the zero-sum game here? Once this paradoxical structure became evident through a long series of thought experiments, a hidden truth became obvious:
Whatever it is, the "new" third pole cannot be framed in opposition. It must therefore represent acceptance -- or at the very least, some form of neutrality.
Unification instead of division.
Peeling back just this first layer of the onion required years of study, long before encountering the other website. "Lifestyle as a method of study" mentioned above takes more time but generates more integrated insights, revealing subtle weaknesses unseen within purely academic, theoretical pursuits. Eventually it became evident that all previous insight into trinary logic was merely a clever reiteration of binary logic structures. That's so important it needs to be repeated:
"All previous insights into trinary logic are merely clever reiterations of binary logic structures."
Truly, a terra incognita was being discovered. There were many more layers of the onion yet to go, but you can see even this first layer of insight has evaporated the "deny opposite absolutes" approach described by the Middle Way Society. Hopefully, its author will come to such realization and find a more amiable middle way[2].
The true trinary approach cannot be about denial of the extremes; it is about embracing extremes simultaneously by organizing them.
Instead of projecting a dual opposition upon the world -- each extreme opposed to its opposite -- true trinary logic understands "extremes" are simply a binary way of organizing. It reorganizes such poles in relation to a third, unifying context. In this light, extremes begin to soften as though touched by "moderation in all things, including moderation."
The test of a first-rate intelligence
Context is important. Note that "unifying" is completely different than "excluding" or "denying" or "opposing" or any other form of division. To do this requires holding contradictory thoughts in the mind simultaneously, which is really difficult for the ordinary person.
F. Scott Fitzgerald put it this way: "The test of a first-rate intelligence is the ability to hold two opposed ideas in mind at the same time and still retain the ability to function." You might think binary-minded people can do two contradictory thoughts easily, but look more closely: "the ability to function" is a third thought process, and that's the key point of Fitzgerald's quote. It's the most difficult part.
Think about times you have contemplated two opposed ideas. If you're like most people, you had to sit and do nothing else while doing so. We're talking deeper than "walk and chew gum" at the same time. You had to temporarily set aside your "ability to function." Unless, of course, you have a first-rate intelligence. For the rest of us, this loss of functionality is a clue about how limited is our day-to-day binary logic frame. It is also a strong hint toward a related insight that binary logic prefers to think linearly. Not planarly, as in two-dimensionally, but linearly, as in one-dimensionally. There's a whole rabbithole behind that ("why does two-based logic prefer one-dimensional paths?") which is explored elsewhere so we'll leave it for now.
Because binary logic engages only the extremes existing at the outer, opposite, edges of a conceptual structure, the only place it has for a third pole is "in between" these extreme outer edges. This works okay, but is an inadequate way of positioning any encompassing structures in trinary logic, where the unifying outside contains the two "extremes." An example can be seen in how a computer works: Everyone knows computers use binary logic, but nobody talks about the clock tick which separates a zero from a one. This tick is a necessary part of the logic, but it's invisible, never seen as a "third thing" which encompasses the two inner extremes. This conceptual structure turns the binary idea of trinary inside out. It places the divided extremities into the center, and puts a unifying context at the edges.
The trinary idea of trinary involves superposition
In binary thought, this structure means the impossible: theoretically, two separated "extremes" must have nothing between them, not even the Law of Excluded Middle standing like Samson between the pillars of true and false. Therefore the extremes... are contiguous...? which is impossible....
The impossibility is resolved when you understand that logical superposition is possible: in true trinary logic, we're talking about polarity as two ways of seeing the same thing, rather than as two separate things. With superposition, the two ways can happen simultaneously, within the same context. There is no either/or, just varying degrees of both/and. Either/or is a subset of both/and, not a competitor. See how we're organizing things now, as mentioned earlier?
Once you transcend binary logic, you find there are actually no true polar opposites, which are illusions cast by overexercising the Law of Excluded Middle. Turns out, in practice the LEM is not a Law, it's a Rule of Thumb which ought to be used carefully, understanding its limits. Nothing is ever perfectly opposed to anything. The exclusion aspect of this "law" is a myth, a phantom, an impossibility, a moving target.
Instead of exclusion, it turns out that within every polarity, one side or the other is more functional (for a given context) than the other in a way that can be easily seen when analyzed from a trinary perspective. In other words, for every pole that exists, there is never a single opposite, but at minimum two other "poles," neither of which are fully opposite, and one of which may be a better fit. Here we begin to see the "three" of trinary logic.
The great 19th century logician C. S. Peirce was possibly the first to notice that logic cannot have less than three fundamental elements, and his observation is woven deeply throughout many of the pages of this site, whether explicitly or not.
Here is an easy way to understand this seeming paradox: "You cannot divide something into two unless you have a third thing which does the dividing." There is a fundamental plurality of polarity which cannot be understood from within a "pure" binary perspective, where its abundance makes no sense. It sounds redundant and absurd: how can a thing have two opposites?
In truth, it can't. It's on a spectrum which wraps around, like a video game where your character goes off screen to the right and immediately appears on the left side. There are no opposites in such an unbounded realm. East becomes West by merely thinking it so (or physically moving to another location), and it all still makes sense.
This is not a manifesto
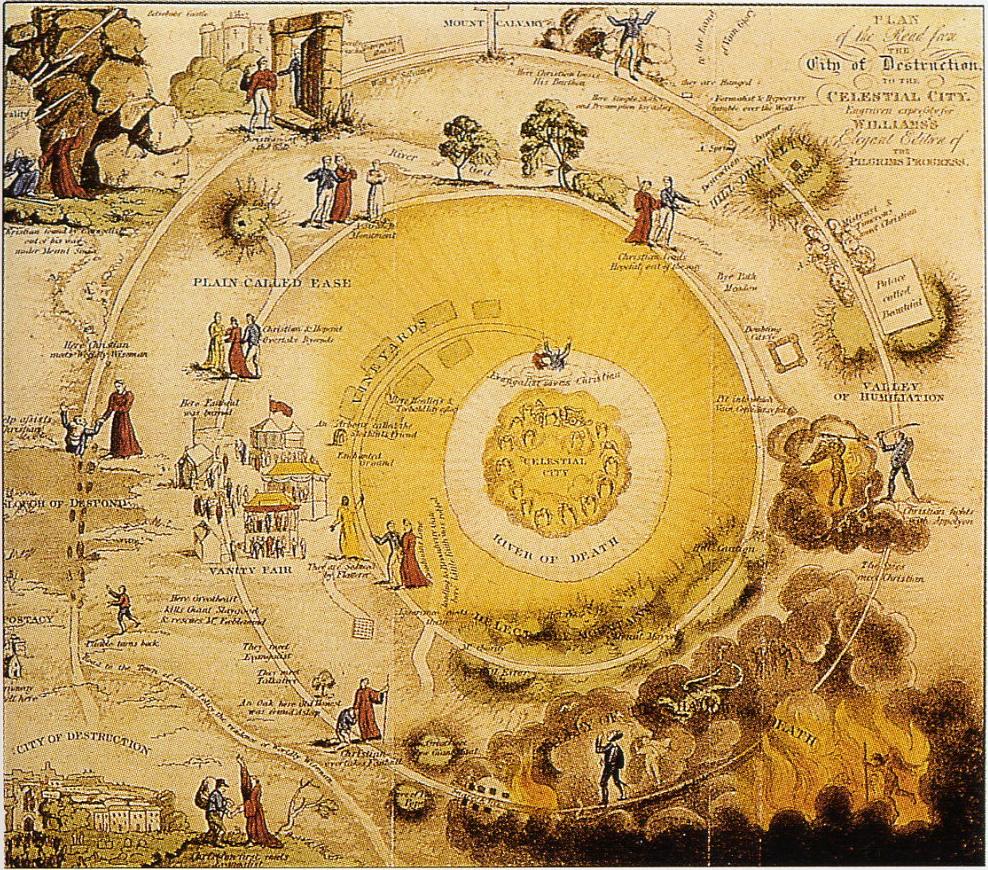
It actually kind of started out as such, as is the way of the world, but time and maturity happened. Eventually the language was updated to make this front page more exploratory than a dogmatic call-to-arms. It's way too nascent to be a manifesto, and these thoughts deserve to be elucidated more carefully before we march. That's pretty much a true statement always, so hopefully no one gets the idea of transforming these thoughts into a manifesto. Remember the journey is solitary and inward, not outward.
There is much to be said here, and the weblog for clearhat.org explores these and related non-binary ideas in an "out of the box" manner, circling around the notion that there exists a little-known terra incognita in plain sight. See the illustration to the right for a map of such a spiral.
Note: not everything written on this website is non-binary. As mentioned earlier, this is ultimately a personal website, not something around which people can polarize themselves for or against. Because of the way of the world, that kind of thing will happen, but there's a reason why the weblog section is called "Rough Drafts."
All of this is written in the spirit of seeking truth via thought experiment, not yet in the spirit of delivering what has been found as truth, although some of what has been found so far falls in the general region of long-sought truths, often found because the trinary angle of approach is unique enough that things hidden in plain sight become visible.
Hence on this site there is a fair sprinkling of perfectly ordinary musings, same as might be found on the weblog of any tech-oriented armchair philosopher or introspective dreamer of beautiful things. Bugs are fixed, tutorials given for obscure techy tasks, and notes-to-self are posted from time to time in a most ordinary way, inline with the deeper philosophical, mathematical, logical musings. Eventually these articles will be collected into a book, where such items can be left out, but for now, here they are.
There are also a few extraordinary things here, too, probably the most notable of these being the most popular page on this site for several years, the ever-growing post on the infinite sphere the center of which is everywhere. Traffic died out ever since a certain large search engine changed their algorithm to downplay personal sites, but it remains a rather intriguing collection of quotations on this subject well worth considering. A good place to start if you've made it this far.
In conclusion, leaving off from words, here is a cool animation found somewhere on the internets one day and assigned to the bottom of this page ever since for no reason at all other than it's beautiful.

Footnotes:
- ^ The link above goes to the "balanced ternary" page on Wikipedia, which is the safest place to send people who want to understand more about trinary logic from an external source. The astute reader may wonder: Why not link to the "ternary logic" page? Well, it will just confuse people. Here's why. Trinary logic is introduced at Wikipedia like this:"In logic, a three-valued logic (also trinary logic, trivalent, ternary, or trilean, sometimes abbreviated 3VL) is any of several many-valued logic systems in which there are three truth values indicating true, false, and some third value. This is contrasted with the more commonly known binary logics which provide only for true and false." It's Wikipedia, so you know this description is roughly the most common way of understanding trinary logic. However, something which is not mentioned in the article is that this definition silently assumes a binary frame to talk about something which is fundamentally non-binary. This assumption is easy to detect because each of the three truth values are separate from the others. The question nobody asks: if these three are distinct, then what fourth thing is doing the separation? In the most common answer, then, there is no discussion of a model involving their unification, blending, merging or superposition with one another. Their distinct separation is assumed without comment even though it is an artifact of the Law of Excluded Middle. This is a "law" required for binary logic but not necessary in trinary. A truly trinary implementation of trinary logic has no excluded middle. In short, the commonly-accepted "trinary" structure is not truly trinary. It's a binary implementation of trinary.For years this website has journaled the development of a truly trinary logic unencumbered by such binary artifacts. Here, the prefix "true" is often added to "trinary" when talking about a three-valued form of logic with an "included middle." The included middle operates in ways which seem nonsensical within ordinary binary logic. For example, in true trinary, things like true and false can blend with each other and with an underlying "oneness" which is unknown to binary logic. The middle region is known as the continuum in binary-structured thinking. Such continuum is believed to have nothing to do with binary logic.To summarize: true trinary logic is not three equal poles: "true-XOR-maybe-XOR-false" or "flip-flop-flap" or "-1,0,1" nor is it anything with three discrete poles. Instead, true trinary logic is comprised of three regions which can be summarized as something like: "true-AND-false," with the AND being the most important pole since it blends the other two. If you'd like to know more about this, take a look at this article where I more fully develop the ideas in this footnote.
- ^ Clearhat is a way which is an implementation of The Way (this does not mean the Tao, which is another well-known implementation). The Way existed before words, so capturing it in words is always a partial realization. For this reason, this is not a manifesto, but a wayifesto. This wayifesto is only one waying of The Way, of which there are an infinite number of ways. The first version, published without fanfare November 4, 2024, is numbered 1.1. This is to emphasize the point that there is no 1.0 for the clearhat way. 1.0 is reserved for the The Way, which exists beyond words. Calling this a manifesto would be like an ordinary subject calling himself king -- while the king still sits upon the throne. That would not be aligning with the way. A good way to visualize the difference between a wayifesto and a manifesto is to imagine the legal difference between a sovereign individual and his legal entity "person" bound to behaviors and consequences by an unspoken social protocol and well-hidden contracts enacted before he was old enough to understand them. There is a world of difference between the two. Since there are plenty of manifestos which describe the sovereign man idea, this analogy is just an analogy revealing a point, not a polemic making a point. In other words, a wayifesto is not a manifesto because the only true "manifesto" of The Way is The Way itself, which existed before manifestation. One exists in a realm of freedom untouched by the legalese which binds the other. Just as you can wake up from within personhood and realize who you truly are is a sovereign who exists beyond the legalese, the clearhat way reveals that you have rights which exceed the boundaries of ordinary rights. But one thing often weakly developed in manifestos: you also have responsibilities. If you attend to the responsibilities carefully, you can keep the freedoms, but if you enter into contracts knowing that you are relinquishing those freedoms, then you lose them til the contract ends. A wayifesto is talking about who you are before you knowingly enter into any contracts, and a manifesto is talking about who you are after you do so. There are other ways to visualize the difference, but this view, one of sitting within a contractual arrangement that was entered into unknowingly, and viewing freedoms which can be had by simply relinquishing The Matrix as the limit of your behaviors, and thereby discovering that others have seen The Way and wrote it up in a manner you could comprehend, is fruitful enough for now.