Here is a small proof that one plus one is equal to three. That is a statement which on the surface seems completely absurd, so to alleviate that first impression, let's carefully establish the logical elements which comprise this proof. Each element will be seen to be logically sound. Then we'll […]
Mathy Stuff and Ternary Logic
This "Mathy Stuff and Ternary Logic" category covers mostly mathematical essays, with occasional forays right into ternary logic, which underpins my inquiry into mathematics.
The binary perceptive lens is not for the purpose of dividing everything, but for the purpose of uniting everything
A recent essay where I invented the word trivulet as the name of the fundamental ternary logic element ended up becoming a fertile field for new insights. This is now the second post derived from ideas discovered while writing that one. While explaining how ternary logic is different from binary […]
On how ternary logic is more fundamental than binary
I just wrote the following in a footnote about how to argue that ternary logic is more fundamental than binary: The "Law of Excluded Middle" is equal in strength to the assertion that there is "true" and "false." This means there are three elements required for binary […]
On why to use "trivulet" instead of "trit" to describe computing with the fundamental ternary logic element
In the ongoing labor to develop an internally-coherent way of perceiving ternary logic -- and its most famous derivative, binary logic -- I have come to an understanding of how ternary logic is the proper logic of the continuum; not of particles, division, or separation. Particles, division, and […]
Upon realizing the Riemann Sphere theory I'm working on is gaining traction independently of me
In a brand new article published yesterday on Medium, Kasper Müller writes about The Riemann Sphere: A world where you can divide by zero in a manner which weaves in some insights that have been the endpoints of several private thought experiments. So as I'm reading the article, not only do I […]
Somewheres about 10,000 hours into solving the Riemann Hypothesis, one encounters Dante's lion, wolf, and leopard
Introduction I'm not good at basic math. I struggle with many things which any decent mathematician aces early. For example, a few elements of calculus still remain over my head, although I have climbed the slopes of that mountain several times. Linear algebra is only just starting to make sense to […]
Most hilarious math paper I've yet read (on p-adics)
I've known about the rather curious set of p-adic numbers for years, even before they started getting famous with perfectiod spaces, but I never knew there were some of the wildest insights into mathematics buried within their "weird" way of thinking. I put weird in quotes here because […]
Upon realizing I independently discovered _another_ new theory in mathematics
A few months ago, I found that one of the more beautiful ideas I had been developing alone for several years had already been discovered by other mathematicians, who had published rigorous papers on the idea. While my own insights were not yet rigorous, they were developed well enough that I quickly […]
On the English Kabbalah, and why Mathematics is better than Kabbalah
first written March 2000; updated 2022 "I just had one of the most rewarding meditations in my life this morning. The letter 'C' opened up for me." My father was driving late one evening, and I was riding. I looked at him. The lines of his face reminded me of Leonardo da Vinci, whose […]
That day when it was clear the amazing Jipidy-Jay was a lot like Ramanujan
I've been training a GPT-J instance to write a cybersecurity blog post, using blog posts I wrote over the past year to help it understand the idea. After a lot of back-and-forth, I got the GPT-J (The Amazing Jipidy-Jay) to write the following: [Title]: Qwerty, 'The' World's Largest Ransomware […]
Upon realizing I independently discovered a new theory in mathematics
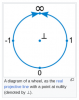
(Note: The two spherical illustrations from this weblog post are taken from a post which I wrote last year; compare with this illustration for Wheel Theory from Wikipedia) It's true that the original discovery by others goes back to 1999, and the first serious paper on this new branch of mathematics […]
ARTHUR M. YOUNG's WHY SEVEN? (TEACHING SERIES) (transcript of video)
This post is explained in the preceding post. Below is a transcript of the following video: ARTHUR M. YOUNG's WHY SEVEN? (TEACHING SERIES) (YouTube) Why Seven? To explain seven we have to go to the torus. The torus is one of the most common phenomena in nature, for example the vortex in air. The […]
ARTHUR M. YOUNG's GEOMETRY OF MEANING (TEACHING SERIES) (transcript of video)
I have discovered the joy of learning Arthur M. Young's remarkable insights. I have not read his books yet, but stumbled into his writing recently, and realized quickly how he is a brilliant intuitive -- indeed he has an exceedingly rare way of seeing the world, with deep insights into the nature […]
Contemplating Fano plane leads to a tetrahedron?
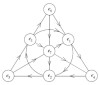
The other day, I was tweaking the symmetry of the Fano plane, as described in a previous post, and ended the experiment by pondering whether there was more to the idea than I could see. A few days passed, and then today, while I was reading a completely unrelated description of energy flowing into a […]
Improving the symmetry of the Fano Plane
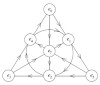
While reading John Baez's article on octonions, I came upon the illustration of the Fano plane familiar to anyone who has studied octonions for at least 60 seconds. I've seen it many times before and pondered again at what riddles remain buried in its symmetrical shape. Then as the article […]
On the ternary nature of the will to meaning
I have been working out the details of the ternary nature of the "will to meaning" which was originally developed within Viktor Frankl's logotherapy, which I believe to be related to Wittgenstein's ideas on language. On a related note, I believe that Schopenhauer's insight into "will […]
Chomsky confirms an element of a developing theory on the ontology of mathematics
As you can see by this third post of the day on the same topic, I'm rather enjoying this interview: Noam Chomsky on Jung, Wittgenstein, and Gödel (Ask Me Anything), and this time I'm not nitpicking his answers, but I find him confirming a hunch I developed as a component of a larger theory on the […]
Another non-answer from Chomsky, this time on the hard problem of consciousness
I'm still digging this interview with Noam Chomsky, Noam Chomsky on Jung, Wittgenstein, and Gödel (Ask Me Anything), but this post is similar to another I made earlier today, wherein he gives a complete non-answer to a question for which I really think his answer would be particularly insightful. […]
All fractions are one fraction
I call my weblog "Rough Drafts" even though some of the entries are fairly well polished, published after weeks or even months of careful writing and editing before release. But in other entries, I write wild stream-of-consciousness gagompoofery like this. This one is so rough it's right […]
Infinity is the backside of zero; they are the same thing
Got it. Been working on this one for a while, I've seen it in glimpses over the years, but it just fell into place. Infinity is the backside of zero. Just like a quarter has a heads and a tails, this thing I've been calling "the origin" for a long time has a heads and a tails. This idea is […]