Introducing true ternary
Ternary logic is introduced at Wikipedia like this:
In logic, a three-valued logic (also trinary logic, trivalent, ternary, or trilean, sometimes abbreviated 3VL) is any of several many-valued logic systems in which there are three truth values indicating true, false, and some third value. This is contrasted with the more commonly known binary logics which provide only for true and false.
As it's Wikipedia it's safe to assume that this is a common way of defining ternary logic. However, there's an important piece missing from this definition. It's something which is not mentioned here nor anywhere else in the article. What's missing is the fact that this common definition assumes a binary frame to talk about something which is fundamentally non-binary.
The assumption is easy to see because each of the three truth values are separated from the others but there is no mention of what fourth thing separates them from each other. Nor is there any discussion of continuity, unification, blending, merging or being superposed with one another. This is an essential ingredient which ought to be in the first introductory sentences. The distinct separation between three truth values is assumed without comment, even though it is a direct consequence of the Law of Excluded Middle, which is well known to be an artefact of binary logic. A truly ternary implementation of ternary logic does not use excluded middles.
In short, the commonly-accepted "ternary" structure is not ternary, it's a binary implementation of ternary.
For more than a decade, this obscure website has journaled the peripatetic development of a truer form of ternary logic unencumbered by such binary artefacts. Here, the prefix "true" is often added to "ternary" when talking about a three-valued form of logic with an "included middle." The included middle operates in ways which don't make sense in binary logic. For example, in true ternary, concepts like true and false can blend with each other and with an underlying "oneness," which are structural concepts completely unknown to binary logic. Such unifying ideas are more common in the East, but in the West, they make little sense. The good news is that this omission was worse a century ago; over the past decades the idea of non-binary is slowly gaining ground and the future finally looks bright for such ways of seeing.
The "included middle" region is known as the continuum within mathematics. But not logic. Because of a strong dependence on the law of excluded middle going all the way back to ancient Greece, the continuum is currently believed to have nothing to do with logic. In truth, it is at the center of all logic -- even binary -- for when you peel back the artificial abstraction we call excluded middle, you find, right at the center, that there is an underlying continuum which holds everything together. Always has, whether we could see it or not. Division itself is forged out of the continuum, which seems like a ridiculous statement until you think about it for a while and realize the opposite is even more ridiculous. A continuum cannot be forged out of division, now, can it?
That small piece of logical argumentum ad absurdum is the tip of a small iceberg we'll leave alone for now. To conclude this introduction, here's a TL;DR: True ternary logic is not three equal poles, like "true-OR-maybe-OR-false" nor "flip-flop-flap" nor "-1,0,1" nor is it anything with three discrete poles. Instead, true ternary logic is comprised of two or more overlapping regions and some rather unusual concepts which give coherence to the seeming incoherence. These can be most succinctly described in the binary frame as "true-AND-false," with the AND being the most important pole, since it blends the other two.
Wait, what? I'll say it again:
From a binary perspective, true-AND-false looks like only two values. But look again and think carefully about what you're seeing. When you can see three where you previously saw two, you're beginning to understand the role of the included middle, hidden in plain sight for many, many centuries.
The superposition of true and false by redefining AND
I wrote much of the preceding introduction while adding a footnote to the front page of this website. Then I realized what I had discovered with the insight about "AND" was deep. I had something deep enough to justify writing a longer article. So here is the article, which is basically a sequel to yet another article I wrote yesterday, where the first hints of this discovery came to light.
I'm excited because I've never been able to see the blending of true and false in the manner that I see now so clearly. For example, I've long been aware of the idea of "Yes, and..." which is related to what I'm saying here. But I always saw it separately, having nothing to do with logic. Here, in addition to being a clever way of promoting creativity and solving many problems, I'm also redefining the way AND is used in logic. Here is how I originally wrote it in the previous article:
"And" is a simple word that conveys the concept of being connected. It also conveys a division, just like "this and that" are separated into two distinct things by the "and." This is why we say "this and that," not "this and more this." In this way, and simultaneously means division and unity. The hidden unity aspect is brought to the surface more than with the word "division."
The distinction is subtle, but there was a lot leading up to that insight, and the subtlety jumped out at me. I realized I had finally discovered how true ternary AND is very different from binary AND. It has (at least) two layers, one which unites, and one which divides. Furthermore, in a recursive manner, the aspect which unites also has two aspects: deep and shallow. Global and local. At the deep end, it is the continuum, meaning it is connected to everything everywhere in a global manner. At the shallow end, it is specifically connecting two logical elements in a local manner. This is how I'm picturing it in my mind.
A picture will help
In fact, now that I think of it, the ternary AND intuitively looks a lot like an illustration I once made to describe the difference between ternary and binary logic. Here, I'll pull it in from the article where I first used it...
Ok. Found the image in this old post from 2019 -->.
That horizontally layered structure in the middle is similar to how I'm envisioning the AND today. Revisiting what is now an old memory, I'm pleased to see that the "ternary logic layer" even references the phrase "contiguous whole" which is another way of saying the continuum.
So this is an idea I've had in mind for about 5 years and now I can see a new dimension of it. If I recall correctly, when I wrote the 2019 article, it was the first time I'd figured out the basic structure in a way I could visualiz... ah yes, now I remember:
This drawing was the 2nd iteration. The one I drew in 2019 was so new to my awareness its descriptive labels were almost incoherent. A couple years later I was reviewing old weblog posts and realized it needed to be annotated better. So I drew this present illustration, with almost completely different text[1].
What's new with today's discovery is the way AND carries both the uniting and the dividing aspects simultaneously[2]. Even though it was right there in front of me, for the first time I see how the "infinite spectrum" I mentioned five years ago works. I've been imagining it as a single layer unto itself, but it clearly has multiple layers.
If I drew this image today, I would flip it over, with the ternary layer at the bottom, because I have since learned that the ternary connection with the continuum happens underneath, or inside everything ... at the center of everything. [Update: I created the newer image; see below. I added a continuum layer.]
Everything connects to the continuum from within
Most people know that what we experience as reality happens along the outer surface of what is happening in quantum physics. What I'm adding to this picture is that the inner "surface" is the continuum, illustrated in the updated image below as the bottom layer (see "Continuum sees all" in the following image). This is an idea which frustrates intuition at first, so let's look at it carefully.
First, note that what I've drawn below is a 2D sketch of a conceptual reality which is probably more... 3D spherical... than linear. I would like to draw the picture yet again to capture this 3D aspect but I'm not exactly sure how yet. I'm still thinking through how it works: I know the order of layers in the sketch is correct, but the actual shape is something I can only picture in incomplete glimpses at the moment.
If the continuum line at the bottom of the sketch shrinks to become a point at the center of a sphere, we're moving in the right direction, but then what happens with the three line segments of "true," "middle," and "false" which are at the top of the illustration? I can only guess something like the following: Imagine that the "true" and "false" distinction is not linear as we think of it, but true represents the "inside" of a sphere versus false as the "outside" of a sphere, with "the excluded middle" simply being the thin surface of the sphere. The nice thing about this transformation is that the excluded middle becomes not a "realm" unto itself as it appears in the sketch, but merely a different way of looking at one of the two realms of true/false.
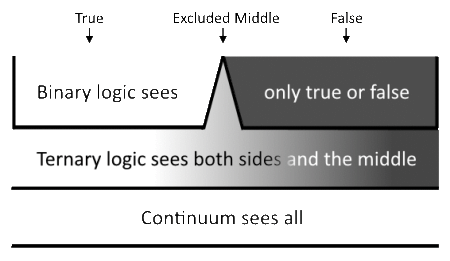Let's consider these ideas from another angle: imagine that the continuum shown here (<---) is at the center of every atom in the universe[3]. We normally think of an atom as containing a finite space but what if the center of an atom is where infinity lives? That would make us... the outer edge of creation, where infinity is fading into nothingness. If matter exists at the periphery of infinity, we live in the final region of the infinity spectrum, where things become finite before there is... nothing.
That may still break the brain (it does break mine), so let's look at it from yet another angle:
Although it is flat and 2D, the order of layers in this sketch should make at least a little bit of sense to any quantum physicist for a surprising reason: Quantum physicists perform an "unexplainable" step while calculating the nature of subatomic particle/waves. It's a step which no quantum physicist has yet been able to explain fully. If you ask questions about it, they famously tell you to "shut up and calculate."[4]
But if you understand the continuum is at the center of electrons and quarks[5], then you can explain the mysterious step!
The step is called renormalization because the mathematical equations which describe quantum physics zoom off to infinity while they're being calculated. However, experiment shows that this mathematical anomaly doesn't happen in reality. So renormalization trims off the infinite part of the calculation, and everything "just works." It works so well that these days few people worry about the odd pass through infinity that happened along the way.
Adding a negative infinity to a positive infinity
I'm clearly an amateur in this area, so forgive me if I get things wildly wrong without realizing it. One site I was reading described it this way: "Roughly speaking, renormalization solves the infinity problem by adding a negative infinity to the positive infinity to cancel it out." This is a nice way to put it, but it poetically glosses over the fact that the "negative infinity" comes out of thin air, which is exactly the kind of magic that mathematics works hard to avoid. But it solves a difficult problem in an elegant way which is proven by experiment to be true, even if the math uses what would be called sleight-of-hand in any other instance.
This is tolerated because the Standard Model of subatomic physics works extremely well. It famously describes its domain with greater accuracy than any other theory in science. But... for all its precision, it doesn't yet know how to handle infinities.
It just seems too absurd that every particle is connected to infinity at its very center. Physicists do try to make this idea work, but none have yet succeeded. For example, one of the great minds in quantum physics, John Wheeler, suggested something like this once to Richard Feynman, but as Feynman noted in his Nobel acceptance speech, they both shrugged it off later... although they did continue to use elements of the underlying thought experiment in other ways.
However, think about it, and you might agree: this is what's going on behind renormalization. All we need is a clever mathematical way to make a path through both ends of infinity and back into our finite reality again, and we'll be able to replace the sleight-of-hand renormalization with something more mathematically elegant. Less hand-wavy, as they say.
Projective geometry does such clever things with infinity, as does the Poincare disk. These are well known ways to reframe infinity. However, I think they hint at a truth which is more obscure. I've explored some ideas around how to get clever with infinity elsewhere on this website, but that part of my journey is still a work in process, so let me "renormalize" this present narrative by getting back to what is happening under the hood with the AND.
The ternary logic of AND is visible in ancient Hebrew
I've known for a long time that ternary logic intersects with the continuum. I've called this different things over the years, and I've studied it from several directions, but I've never before seen it with the clarity I do now.
Now I have a good visual on a "missing link" which holds everything together, and how to capture this understanding by simply deepening the definition of the very ordinary word "and."
As explained in the other article I wrote yesterday, "and" is a simple word that obviously conveys the concept of being connected. We're quite familiar with that aspect. But what is little known is how "and" also conveys a division. The example I gave is how "this and that" can be separated into two distinct things by the "and." This is why we say "this and that," not "this and more this." The "that" is divided from the "this" equally as much as it is held together by the "and."
Hm... As I'm editing this a few weeks later, that example seems like a stretch, so if you're puzzled, the idea will become more clear with a better example of this dual role. For another example, let's take a look at how "and" is used in the oldest parts of the Bible.
The first letter of nearly every sentence of the first five chapters in Genesis is the letter Vav, which is translated as the word "and." This usage of "and" is most common in Genesis, but also happens frequently throughout the rest of the Bible. This "and" has the same dual function of UNITE and DIVIDE that I'm talking about here. It acts like punctuation, separating two different thoughts. But it also acts like a bridge, uniting those two thoughts.
And the earth was without form, and void; and darkness was upon the face of the deep. And the Spirit of God moved upon the face of the waters. And God said, "let there be light": and there was light. And God saw the light, that it was good: and God divided the light from the darkness. And God called the light Day, and the darkness he called Night. And the evening and the morning were the first day. (Genesis 1:2-5, KJV)
Note the Hebrew phrase "עֶ֥רֶב וַֽיְהִי־ בֹ֖קֶר י֥וֹם אֶחָֽד׃" translates literally to "evening and morning day first" which is how Hebrew phrases "the evening and the morning were the first day." This is probably the clearest example of separating a pair: "evening and morning" while simultaneously joining them into a single: "day".
Wait.
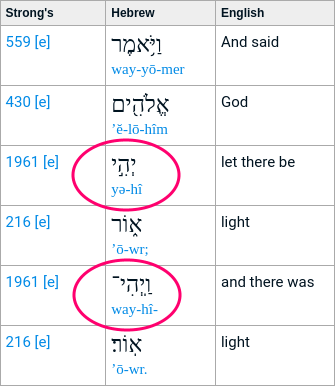While researching that last paragraph, I found an even more clear way! The difference between these two aspects of vav is so clear in the original Hebrew that there are two distinct types of vav, the vav-conjunctive and the vav-consecutive.
- vav conjunctive (Vav Hachibur, literally "the Vav of Connection" — chibur means "joining", or "bringing together") connects two words or parts of a sentence; it is a grammatical conjunction meaning 'and'.
- vav consecutive (Vav Hahipuch, literally "the Vav of Reversal" — hipuch means "inversion") indicates consequence of actions and reverses the tense of the verb following it.
The reversal aspect of vav is fascinating. Hebrew verbs tenses involved are perfect (action is completed) and imperfect (action is ongoing). This means the vav-consecutive either completes an ongoing action, or re-activates a completed action to its ongoing state. The first example of this in Genesis is when God says "Let there be light and there was light." It works like this: "Let there be" becomes "and there was" by the addition of the single letter vav. This is the vav-consecutive.
Hm... While the reversal is fascinating, it does not exactly map to my new insight about the dividing aspect of AND[6]. Compared to my insight, it seems there is more power in the Hebrew idea -- the Vav of Reversal is not simply dividing, it goes further, to reversing a flow of energy. Reversing energy requires energy; therefore the vav has some kind of life within it, more than we usually think when we think of a clinical, set-theoretical type of division.
The AND may go deeper than I realize. Is there an aspect of divinity embedded in the vav, something which judges or revives? Note that the vav appears in middle of the Tetragrammaton. I don't have a clear intuition on all this yet. As I continue to think aloud here, what I'm aiming for is a logical structure that should be findable in ancient sources, but is this the one? It looks like I need to study out the reversal aspect of vav and understand how it functions on a deeper level.
That is for a future thought experiment, pardon the pun on changing tense.
Back to the ternary logic of AND
One thing that is starting to dawn on me is that the new understanding of AND has a vertical action, compared to the horizontal way we normally think of AND. To clarify: By horizontal I mean two equals are being united/compared. By vertical, I mean two layers of abstraction are being united. Or maybe a better way to say it: two layers are being united/compared in the way metaphors unite/compare separate things?
For a visualization of what I'm imagining with the AND, I modified the previous image to show how the AND touches all three vertical layers of the previous illustration. In this tiny word "and", we have the familiar binary union of "thisandthat," the newly-realized ternary division of "this and that," and because of the renormalization discussion above, we can see that AND also touches on the "infinity layer" called continuum in the previous image. The vertical and horizontal dimensions are all here in this image.
In fact, given that description, it is more accurate to say that AND arises from the continuum. Like the invisible peak of the "excluded middle" seen at the center of the top layer, it is the tip of the continuum peeking out on the ordinary world's divided appearance, holding things together. This fits well, because in other thought experiments, I've seen that it is part of the nature of the continuum to be hidden in plain sight. Being everywhere, it is usually overlooked, taken for granted[7]. It also even touches on my previous musing about how there might be something divine hidden within the vav.
I hope with this emphasis you're beginning to see how important the AND is.
Logic gates may be a good way to make these speculative thoughts more rigorous
As I've been thinking about the AND, it's natural that I would think about the OR, which is another fundamental binary logic gate. Along with NOT, which is a simple unary inversion (on=off,off=on), these three are the core of all binary logic gates used in computers today. This new insight about AND makes me want to look at logic gates more closely than I have before.
The next part of this article is going to be even more exploratory than what I've written thus far. I know there are ternary logic gates out there on various websites, but because of the "binary frame" issue mentioned earlier (i.e. non-binary information is often presented in a confusingly binary frame), I've never been eager to study ternary logic gates developed by others.
Paradoxically, I'd rather come at it this way: analyze the few existing binary gates, extrapolate from underlying ideas to a hypothetical "ternary frame" by myself, and THEN compare what I find with the work done by other ternary logic researchers. This may seem to be the long, difficult way, but I've learned that if I develop an intuitive sense of a given ternary idea on my own before I research what others are doing with it, I can more quickly spot binary artefacts and zero in on the true ternary ideas. If I don't do that, I go in circles for days or even years trying to sort out where some other researcher got things wrong and what they got right.
So if you're still with me at this point, let's take a look at some basic binary gates and think about how these ideas might be implemented in ternary logic. I'll be "thinking out loud" here, so fellow speculators will enjoy the journey but others might find this tedious.
AND gate:
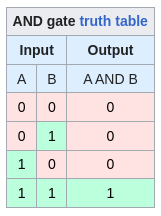
The first row, where A and B are both zero, outputs a zero. The gate "passes through" the zero. It does the same with the last row, where it "passes through" the ones if both A and B are one. This last row is why it's called AND. It clearly conveys the concept of UNITE. Look at the middle two rows, though. See the asymmetry in the output column? Both rows result in a zero. This is a very binary thing, forcing a 0 when it could go either way. This arbitrary structure has the "feel" of other binary artefacts that I was talking about earlier[8]. My initial intuition is that a ternary logic version of this gate would be more flexible with the output of these two middle rows, but it might require more context to determine whether to output a 1 or a 0, maybe along the lines of how a memristor works, since it carries the extra context of a previous state...? Lastly, if three ones makes a UNITE, then three zeros in the first row are more like a DIVIDE. Might want to pick up that thread later, if zeros keep equating with the concept of DIVIDE.
OR gate:
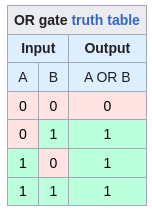
Aha. Here's what happens if those two rows output ones instead. This is the first time I've realized OR is the same as the AND except the two middle rows generate ones instead of zeros. In previous thought experiments, I've only lightly considered OR and XOR, observing how the strong exclusion aspect of the XOR is a very Law of Excluded Middle kind of concept. But looking at this truth table, seeing the output is 1 if A OR B has a 1, makes me think it's more friendly than I realized. I honestly never noticed that an OR is basically an upside-down inside-out AND. (If that last sentence doesn't make sense, I agree, but while editing these words I keep seeing glimpses of a vertical inversion which I don't know how to put into better words yet). Note that XOR is similar but it makes the output 0 on the last row, which does convey that binary exclusion more than this plain OR. The only other thing I notice is that the OR gate passes through the ones more than the AND, making it less overall divisive, in keeping with the thread I mentioned earlier. In other words, if the logical DIVIDE is what happens when the output is zero, the OR gate ironically has more opportunities to UNITE than the AND gate. Maybe I'm looking for a nomenclature change as I develop the ternary gates.
NOT gate:
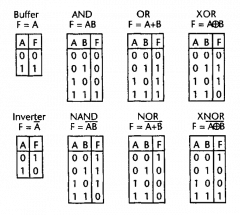The picture for this truth table shows the whole set of all possible binary gates so you can see how simple the NOT is in comparison to the others. It's the one called "Inverter" here. It is a unary gate.
Wait a minute... if we think of AND more simply -- as a unary gate with two rows instead of four like the normal AND -- outputting a one only if it has two 'one' inputs, then... the unary AND (called "buffer" here) is simultaneously the wire between all gates.... and the bottom row of both the AND and the OR gate...
Hm, who would have thought the NOT gate would lead me to a unary AND? I'll come back to this unary pair, the inverter and the wire, later. (Ah, yes, and a few days later, I've inserted the composite picture and added the parenthesis above because what I'm calling the wire is known as the "buffer gate," although I don't know why yet.)
NAND gate:
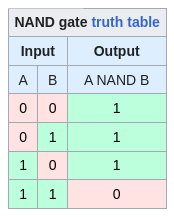
If the OR is an AND upside down, this is a horizontal inversion (literally NOT-AND) of what's happening with the AND gate. Except for an additional NOT I don't see anything notably different from my preceding analysis of the AND. This is also known as a "universal" gate because all other gates can be made from it, but the inefficiency of that idea strikes me as... inefficient. Like the OR is a mirror of an AND, the mirror of NAND, called NOR, is also a universal gate.
That's about all for the NAND for now.
Ok.
I now have a rough sense of how these binary gates work through a vaguely ternary lens. I know with balanced ternary we get a lot more gates because that third input column gives us a lot more combinations to choose from. I think I'm ready to take a look at the actual ternary gates and figure out which ones map best to the new insight with AND and its simultaneous UNITE and DIVIDE.
All ternary gates
This is a single table containing all ternary gates. Right at the beginning I'm struck by the beautiful symmetry visible in how these 81 cells are filled:
input | 0 1 2 3 4 5 6 7 8 9 A B C D E F G H K M N P R T V X Z
------|------------------------------------------------------
– | – 0 + – 0 + – 0 + – 0 + – 0 + – 0 + – 0 + – 0 + – 0 +
0 | – – – 0 0 0 + + + – – – 0 0 0 + + + – – – 0 0 0 + + +
+ | – – – – – – – – – 0 0 0 0 0 0 0 0 0 + + + + + + + + +
That central peak of zeros aligns really well with the central peak of the illustrations I made above. However, this is a meaningless coincidence because they're not really related. This is just an illustration of all the possible ternary gates, not a single structure, unless I can figure out a way to cohere them all together...
Life happened, and I took a break for a week or two, researching around these ideas from time to time.
I've come up with an entirely new way of thinking about ternary gates, quite different from the binary approach we've been looking at together. The intuition that ternary gates are very different than simply binary-plus-one became more clear. While researching ternary logic gates as I just described above, I stumbled into a rabbit hole involving memristors. I quickly realized the memristor behaves closer to what I envision for ternary logic. It's not a purely binary thing.
Because memristors remember their previous state, they behave in a manner more analogous to the way a neuron works than any of the binary gates. I then began to contemplate ternary logic gates from a brain-neuron perspective. That led me to an AI neural net line of thinking. That soon brought me to discovering something remarkable, and it surprises me that I never heard of it before: "the XOR Problem." Researching this turned up some great insights, aligning well with previous intuition. For example, it turns out XOR is another way of saying "excluded middle." We'll come back to that in detail, but before we do I want to unravel the way the Excluded Middle works so you can understand this point with clarity when we get to it.
The Law of Excluded Middle is not logically unary
You cannot "exclude a middle" as a unary operation, nor even as a binary operation. Think about it carefully and you will see. Here's how: We normally think of the excluded middle as being an extremely fine line between two extremes (such as "true" and "false"), so fine that it doesn't really exist. It gets mentioned briefly while defining binary logic, and then plays no role in truth tables or any other analysis or discussion. But no matter how fine you make that line, upon close analysis you must face the fact that the excluded middle -- just like any other line -- requires two outer edges and a middle in order to exist. This makes for a total of three elements.
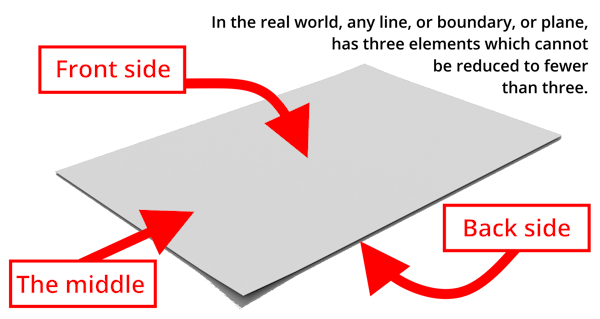A good way to picture this is to imagine a sheet of paper. We tend to think of a piece of paper as a single thing, but rendered logically it is three separate logical elements. It has front side, a back side, and a middle (see the illustration).
This is hard to see separately if you think of things using binary logic -- which everyone does -- because binary logic compresses the logical nature of middles, reducing threes into twos in order to fit the binary model. Then sometimes the twos are compressed even further, into ones. This is where a lot of paradoxes arise, which are easily untangled by using ternary logic to identify these "hidden" elements. In other words, by assuming that the Law of Excluded Middle is a unary operation (as it is normally assumed when defining Boolean logic, for example), we obscure the fact that it's actually a ternary operation.
Calling the same thing by many names and assuming they are different
This took me a dozen years and hundreds of thought experiments to sort out, so anyone who is still reading is to be commended for persistance, because these ideas likely seem nonsensical on the surface. However, there is a rigorous logical system being exposed in this casual manner. For an example confirming what I'm saying, here is the best, most rigorous treatment I've seen on the equivalence between: 1. The Law of NonContradiction, 2. The Law of Bivalence, and 3. The Law of Excluded Middle. The author does an excellent job of showing how all are essentially equivalent, but even he does not yet see: 4. The Law of Identity as a fourth variation on this same theme of separating things from other things.
If you go to Wikipedia you'll find #4 combined with #1 and #3 as three separate things. Look closely and you'll see, underneath the hood, #2 and #3 have been combined, so these three separate things are the same four I just identified above.
This is kind of combination and reorganizing is confusing til you realize that all four "laws of thought" reveal different variations on the same underlying "separating things from other things" theme. At heart, they have the same functional purpose. This equivalence is shown rigorously by the author of the Reddit post linked earlier. The first response to that post shows the confusion which results from the problem I mentioned at the very beginning of this article 
(with Wikipedia talking about ternary logic as if it were binary). True ternary works as I'm describing it here.
There are other examples of people making the same observation. Even AI makes this mistake. But carefully read the illustration to the left (from Quora's Poe AI) and you'll see the Law of Excluded Middle is essentially saying the same thing as the Principle of Bivalence.
The XOR Problem, which caused the first "AI winter"
If that didn't make sense but you're still reading, it will help to see this three-sidedness in the way it occurs within the famous XOR problem. The "XOR Problem" is a well-known issue with XOR which appeared in the field of AI in 1969.
I was delighted to discover it recently, because it so completely confirms my negative intuition about XOR mentioned earlier in this article (when I was analyzing the OR gate). As I continued researching, I was pleased to find that my own previous thought experiments about the Law of Excluded Middle had revealed the same problem as XOR in how it requires a "hidden" assumption to operate. As discussed above, the "hidden layer" needed to render XOR makes its operation necessarily ternary, not binary or even unary, like it seems on the surface.
Remember that I mentioned earlier XOR is a direct implementation of the Law of Excluded Middle. They are logically identical. The problem with XOR was discovered while AI researchers were working with perceptrons, which are the earliest electronic neurons, invented in the 1950s. So here is the problem:
Unlike other basic gates, XOR requires not two but three layers of perceptrons to operate. The other basic gates such as AND and OR only need two layers, an input and an output. When this requirement was formally proven in 1969, the discovery started the first "AI winter." Many people gave up on AI, and funding dried up. People couldn't figure out how to solve the problem. It was obvious that neural nets were therefore only effective for trivial problems.
The solution turned out to be fairly simple. First, it was discovered that an XOR could be built with an OR, a NAND, and an AND, operating in three layers, like this illustration I made (using draw.io, inspired by this excellent article on How Neural Networks Solve the XOR Problem):
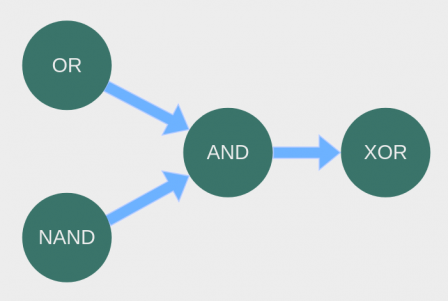Note, to this day, this middle layer (AND in the image to the left) is called "hidden" to distinguish it from binary perceptron "input" and "output." Of course it's "hidden." It's not hidden, it's ternary! However, nobody thought to call it "ternary," which would have hastened the day that the beauty of ternary logic came to the surface.
While this step of development was fairly easy to figure out (people saw it within a year), nobody knew how to train such multiple layering.
The answer was backpropagation, which people understood theoretically even then (historically it traces all the way back to Liebniz), but nobody knew how to make it work.
It was more than a decade, well into the 1980s, before researchers started to figure out how to use backpropagation properly. Once deeper neural nets using backpropagation began to solve the XOR Problem and other large pattern-recognition problems, the AI winter concluded.
Speaking of conclusions, let's conclude this article
Now you have three distinct examples of what I mean when I say that the Law of Excluded Middle requires three logical elements in order to operate: 1. The illustration using a piece of paper, 2. The links to others in math and logic discussions talking about the same core insights from a different angle, and 3. The Law of Excluded Middle Problem XOR Problem with its very obviously hidden ternary resolution.
These three examples provide plenty of material for people who want to dig deeper into these discoveries. I've studied the underlying patterns for years and feel certain I'm right, but I'm open to criticism from people who take this seriously.
I want to write now about insights I've discovered in how memristors within an AI neural-net environment reveal a great example of how ternary logic works. However, the insights are very formative; I need to research more and do some thought experiments to refine the points I want to make. What I'm already seeing is far better than anything observed in the binary gate analysis above, so this is the direction I'm now headed.
This article has already gone out on a speculative limb once, and although we found it to bear fruit, the article is quite long as is. Really, it should be divided into a couple separate articles, but as all of my articles are filed under the heading "Rough Drafts" I think the appropriate thing to do now is to conclude here and start writing another, where I continue investigating ternary logic gates in a way quite different from anything I've yet seen in the world of ternary logic.
More soon, stay tuned.
Footnotes:
- ^ Wow. I just read my own fine print in the illustration, and it looks like I was saying nearly the same thing 5 years ago which I wrote above at the beginning of this article. It looks like that illustration marks a turning point in my ability to express these ideas consistently over time.
- ^ Months after writing this article, I'm reading it again and lightly editing it for clarity, when I get to this sentence. Now I can see clearly that the new insight is best understood as adding a 3rd dimension to the illustration. By that I mean the duality embedded in the AND is best framed by adding the Z dimension to the X and Y shown in this illustration. Imagine two sheets of paper stacked neatly upon one another. The illustration is on the bottom sheet and the top sheet simply has the word AND written on it right about where the number "2" is in the illustration. This vertical stacking is the correct way to understand the way the AND works in a non-linear manner. I'll probably need to write yet another article on this subject to capture this aspect better, but for now there's this footnote.
- ^ To be more precise, it's at the center of every quark, neutrino, photon, and electron, since these are more fundamental than atoms, but "center of every atom" is close enough to carry the point I'm making.
- ^ That's a quote which has been attributed to Richard Feynman although it was N. David Mermin who first said it. If it's new to you, follow those two links and you'll see it's quite well known. One commenter even traces it back to Leibniz who said "sit down and calculate" when proposing a future computer that would be able to calculate the answer to any question.
- ^ Quarks are at the center of protons and neutrons, which along with electrons are at the center of atoms, which are at the center of molecules, and so on to cell, organ, body... every structure in the universe.
- ^ In a sort of footnote to a footnote, I find my new insight is found in Hebrew. It's in this link to Gesenius, who wrote in exhaustive detail about such details: "The imperfect consecutive sometimes has such a merely external connexion with an immediately preceding perfect, that in reality it represents an antithesis to it." I now want to learn all about the Vav of Reversal.
- ^ For a clear example of what I mean here, Isaiah 53:2 says, in a description of the person who best represents the logical concept of continuum: "he hath no form nor comeliness; and when we shall see him, there is no beauty that we should desire him." Strange thing to say of one whose role in the larger story is so... beautiful.
- ^ For example, consider how multiplying two negative numbers makes a positive, which is a peculiar asymmetry rooted in how negative infinity evokes the ancient idea of horror vacui, but that's a story for another day.