Clearhat

This post is explained in the preceding post. Below is a transcript of the following video:

ARTHUR M. YOUNG's WHY SEVEN? (TEACHING SERIES) (YouTube)

Why Seven?

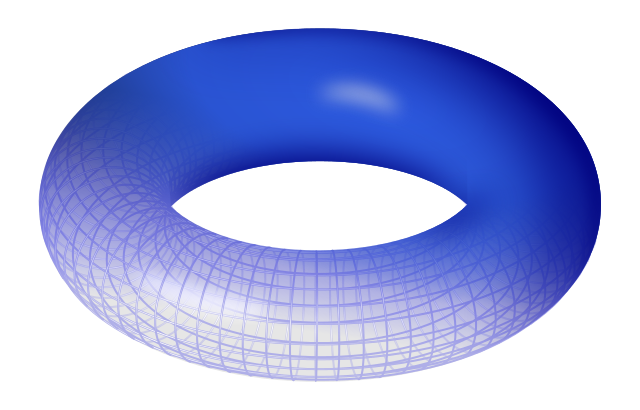
To explain seven we have to go to the torus. The torus is one of the most common phenomena in nature, for example the vortex in air. The tornado is a vortical or toroidal motion. Again eddies in water. The magnetic field is toroidal in shape. The torus or vortex shape has a unique property that it's the only thing that can sustain itself and is the only thing that is made out of the same substance as its surroundings. In other words you can have a tornado which is made out of nothing but air. The tornado is in air.

If you were to try to talk about how to explain a universe from nothing the toroid shape or vortex would really be the only one you could call on, because if you said: "Well it's spherical," then in order to have it made out of the same substance -- not have two different things like a sphere of putty and a lot of air -- you would have to say that: "Well there's a condensed condensation of fog in the middle of the fog." But that condensation would rapidly dissipate, whereas a torus or a vortex, like a smoke ring, will continue to exist even though it's made out of air, in air. So we have good reason from a purely physical point of view to give special attention to this vortex or torus.

However there's a much more impressive reasoning to me that the torus is the shape that the universe must have, which is that it's the only way you can explain a number of metaphysical problems. Perhaps the oldest of these problems is: "How can there be free entities in the universe run by God?" Well, relativity has no reference to God. The same problem comes up: "How can you have the discontinuities of quantum theory within the continuum, like if everything is cake how can you have raisins?" In other words the dichotomy between the particularity of the raisins and the generality of the continuum, or the cake, remains a dichotomy. You haven't really got to the bottom of things until you've explained the bottom, the dichotomy, in terms of one thing.

Well for this the torus offers the solution and the solution is as follows. Suppose if I had a plane. Just imagine a plane surface and there's a dot or a man on the plane. Then I make a cut all around the plane and separate that piece of the plane. Then I've separated the man from the rest of the plane. I've separated this entity from the rest of the universe. Now this would be an either-or proposition: Either that man or that piece is part of the plane or it's separate. You can't have both. But with the torus you can have both and let me show you how that would be the case.

Here's a little blemish that I could call a man. Can you see that all right? I'll make it a little more definite by putting a line around it. This represents some unique entity that's all by itself, but of course it's connected with everything else. The only reason you say it's by itself is I've just drawn this line. But that's just ink it's not -- it's still connected. But suppose I cut around it with this brown line.

Now I've cut all around it. The only difference I've made is that I've included this hole. Of course this hole can be infinitely small and the whole thing can be compressed down, but the principle involved is that I make one cut all around this entity. Now you'd have to imagine my unfolding this from the brown line, separating it all out, and you see that this thing would still be connected to everything outside the brown line, because you could go around through the hole and come up again on the other side of the fence. Here's the fence all around. But I can still get from here to any place outside the fence by going through the hole. In other words this entity is connected with the hole and also separate from the hole. I call this pseudo separation and it's that pseudo separation we have when we create the ego.

In the third stage the separation was represented by a circle with a dot in the center. It was the principle of identity: The principle by which this thing can be given enough distinctness to be able to say it has identity and is distinct from its surrounding. But it's only a pseudo distinction, because as we see from this going through the hole it's still connected -- connected as it were -- by a sort of umbilical cord. Now we can't expect this umbilical cord to be a visible thing the way this microphone line is, where I'm connected to the sound system, or the lights are connected to the power lines. The umbilical cord is non-physical.

It is in those two upper levels that we said were projective are the two upper of the four levels.

Well let's look a little more what else does the torus tell us about this universe, agreeing that it's a possible and even preferable model because it complies with these requirements that we mentioned.

Well this brings me to the coloring problem. The coloring problem is a basic characteristic of surfaces. In fact I can show in this diagram: two orders of surfaces already.

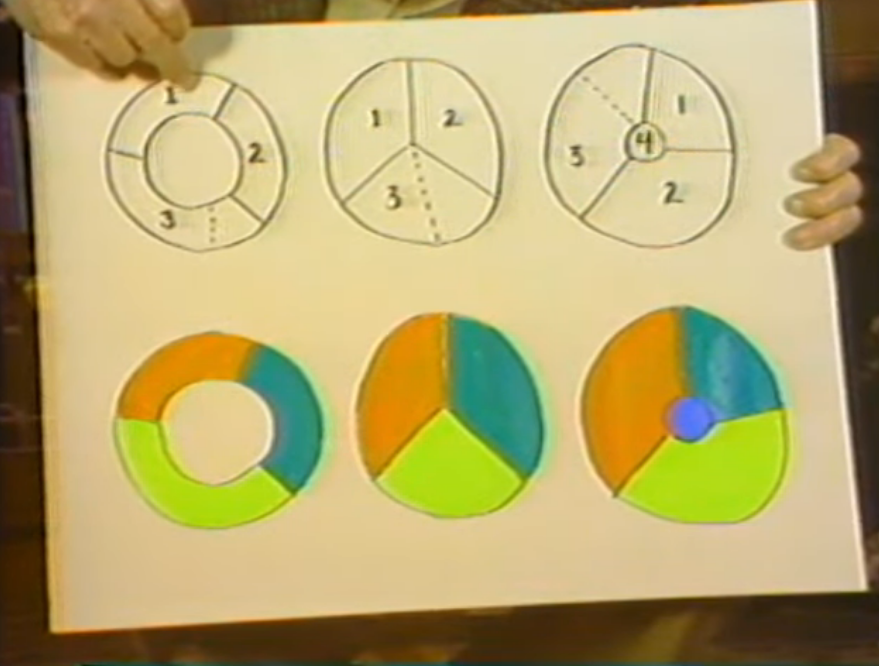
Imagine that this first figure, this one and this one, is a line rather than a surface. I've given it width so I could clearly show areas but think of this as just a ring. Now to make distinctions on the ring, I need three colors, because in this one where I've drawn three things each one touches three, and that's also two. Two touches three and one three touches two and one. So I need those three colors. That's the way it's shown here. If I'd introduced a fourth area, let's say where I've made these dots here, call that four, then that is not touching.

I could use the same. It's not touching one so I could use the same number one. One for this and one for this, and since I've also removed the contact between three and two I could color it with just two colors: one and two. So I don't make it more difficult by adding this area I make it simpler, and if you explore you'll find that only an odd number of sections will require three; an even number of sections will require only two.

Now suppose we go from this which is a line going around a circle to a plane. Here's a plane and I've divided it in three segments as before.

If I were to try to stick in a fourth one again, I would have separated, I would have created a situation where I could color both this and this with the same color and this and this were the same. So instead of using three I'd only need two colors so I don't get -- I don't exhaust -- the possibility of coloring by this process of making more segments. However, moving to this diagram, if I put a place in the center then I have to have four colors because you notice that four touches one touches two and four touches three. Similarly one touches two, three, and four.

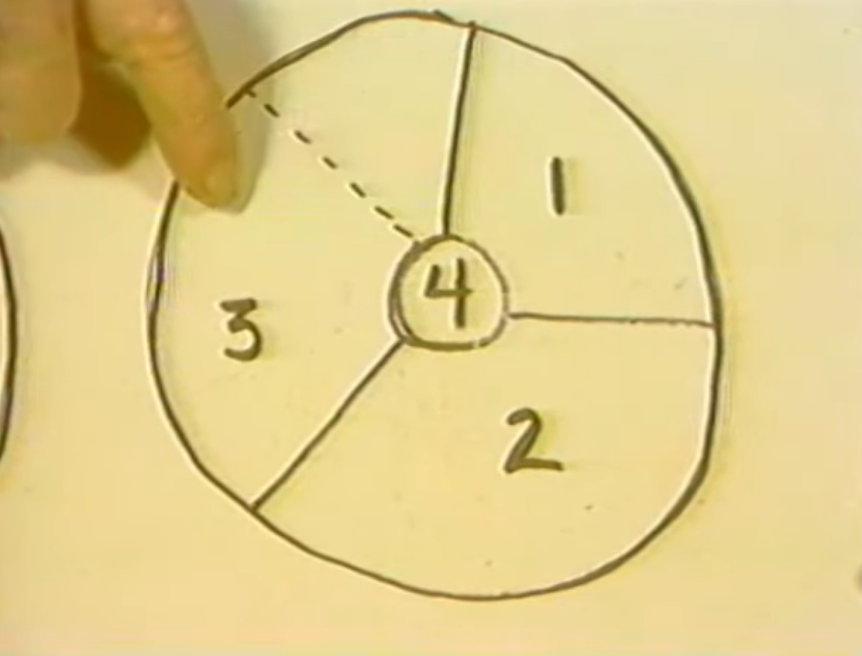
As before if I were to stick in an extra one and try to say: "Well I'll need a fifth color," I've separated it so now that I could color two here as well as here. This three and one could be the same so I'd only need three colors. So we get to the theorem that more than four colors is not necessary for a plane. This is the famous four-color theorem. I don't know what whether it's been proved now or not but no one has ever succeeded in making a map that requires more than four colors. You'd think it would be easy to prove but you see there's always some joker who comes in and says: "Well let me put a country in here," and then you find you have to recolor the whole thing. Now the problem is can you prove that whatever this other person does you will still be able to color it with four colors? That proof may have been done by computer but it hasn't been done in any clean simple fashion.

I don't like to leave it without mentioning that I believe this four-color problem for the plane is equivalent to what I outlined in both The Geometry of Meaning and The Reflexive Universe, that there need be no more than four levels, no more than four distinctions, two dichotomies, to describe any situation. This doesn't mean that's enough for a universe but it means it's enough for a mapping. A mapping, that is to say, a description of that universe.

Well then comes the torus and the torus has the unique property that instead of four colors like this, and I should also say that the sphere is like the plane, it requires no more than four colors. The torus requires seven. Now as I roll this around you'll see there are seven colors and that each color touches every other color.

Now maybe that's too much to see all at once but if I stop for a minute: Suppose I take yellow. On one side is purple, another orange, and here's the gold, here's the green, here's the red, and here's the blue. So there's six colors touching the yellow. In other words, seven colors. That's the same wherever I turn. If I take the purple then it's outlined by blue, by green, by the gold, by red, and then we found on the other side by yellow, and orange. So there's six colors around the purple and this proves the seven color problem.

"Well what about colors, that's just a trivial thing," one could say. Well it's not a trivial thing. It's very profound -- you can replace it by the problem of connecting points with lines that do not cross. You'll find that only on the surface of the torus can you connect seven points with lines that don't cross. It's the same as the coloring problem.

Now what this really means is that the torus or topology of the torus, the surface that has this two ways that it goes round, provides the possibility of more kinds of interrelationship than the sphere and is therefore, from that point of view, ideal for a universe.

Now this takes us into a rather long excursion to describe these properties that emerge.

See what I'm talking about is that the colors are not merely colors. They're interrelationships. Any relationships are very important. Let me go about this in a leisurely way because it's a rather complex subject and you'll get all mixed up if I don't lay some groundwork. For that purpose I have this chart which begins with the simple.

These are the four levels according to the theory of process. As we described before, the first principle is represented by the point, the second principle by the line, the third by the three points or plane, because three points determine a plane. Three points also determine a circle, which is another way of representing this third principle: a principle of identity that I referred to just a minute ago. Then we come to four points: one, two, three, four, which when joined create the tetrahedron. It's like a pyramid. This is the base, this is the apex. The dotted line is the line behind. That's the first solid figure. It's a figure in three dimensions, so we're down to the universe in which we're living. This universe of objects -- and I think I mentioned in The Reflexive Universe that we go further when we can go further with more dimensions, but if I continue with this representation, that is to say, point line playing solid, then I get a figure that doesn't have any name. It's a figure that would be impossible to have in physical space because there are five points each joined by each pair joined by a line.

That means that even to draw it I have to represent one of those lines, well actually represent two of them, dotted, see. But suppose it were in ordinary space then it would be like two tetrahedrons base-to-base. See here's the base and this is the vertex of one and that's the vertex of the other. Well that's all very well. That's very clearly a solid figure with one, two, three, four, five, six, seven, eight, nine, nine edges. And every edge joins two points. But what about the top point and the bottom point? You see in order to join them I have to have an edge that's in the interior of this figure, that's the one shown by the dotted red line.

Now if you were making this out of pieces of equal length you would get along fine until you came to that last one. That last one would have to be stretched. It has to be longer than the other, the others. Well even if they're not the same length it's impossible in practice to make that figure with this extra diagonal without causing what's called redundancy. In other words the position of these two points, the top and bottom, is overdetermined. The lines around the outside are telling it to be in one place and this vertical line is telling it to be in another.

Now this, in structures, as I said, is called redundancy. But it causes an internal stress in the structure and it's very dangerous. You have to be careful to design a structure so that it's not overdetermined, it's not redundant, because it can even break itself. That's why bridges are supported on those roller things so that they're free to move due to change in temperature. You don't want to determine the thing too much because then it'll break just by the change in temperature. In this case this figure could have so much stress in it that it would break before you put any load on it, so it'd be useless as a structure.

On the other hand, we can look at this in a positive way and say this is a way of storing energy. In other words think of this as a spring. This red line as a spring we can now stretch the spring and store energy. This could be a sort of diagrammatic model, a theoretical model, of a mouse trap or a wound-up spring, something that's containing energy, but to apply it more generally, I say this is a model of a seed, because the seed contains energy and this energy is what starts the speed of the seed growing, makes it possible for it to put out the first leaves and then draw more energy from the sun, and then of course it continues on with its growth.

But the original seed had some stored energy in it, that's why we eat seeds because we draw that energy, beans, or oatmeal, things like that. Well you recall that this fifth place was that to which I assigned plants. So it's quite suitable that the five-pointed, five vertices figure, which I call the pentaverton -- because I'm counting the vertices. Normally you would say pentagon meaning you're counting the sides but since one of these sides is concealed and anyway there are 10 of them I call it the pentaverton. I'm just counting the vertices.

Well that becomes then a symbol or a way of describing the abstract principle of growth, a principle that can contain energy, can store energy. Four is the principle that makes a structure. Five is a structure plus contained energy. Now we can go on and ask: "Well what happens when we move to six?" That's six points, it's either four around the middle and a top one and the bottom one so that makes six. But now we have to have three diagonals. We've jumped from one diagonal to three diagonals. I really don't know how to interpret that but since I have animals here it's very tempting to relate these three diagonals to a kind of multiple stretch thing. Okay and it's this -- well the girdles are made out of two-way stretch -- this would be a three-way stretch, what the animal has to have in order to be able to move, because in order to move he changes his shape and that means that something is stretched. In fact you have to stretch in all directions to have this movement. There's some other things that are very interesting but perhaps I better come back to them.

Now might as well follow the course which would be to come to seven. Now when it comes to drawing the picture of seven points with all the diagonals, because when you put -- one way to do it would be to put this seventh point right in the center there. Then you'd see, you'd have six more diagonals, internal diagonals, internal edges, and that would so complicate the drawing that you couldn't see what was what. So I'm going to try to do it in front of you so you can see what is going on. I hope I can make it more understandable instead of more complicated. I'm going to do this in a different way because it is simpler to draw and I hope simpler to understand. I have a circle here with seven points.

Now the problem is to draw triangles such that no two triangles share more than one point. This is also given as the problem of the committees: you have seven people and you want to make seven committees such that no two people are on more than one committee. No pair of persons are on more than one committee. Now if I start out with my committees or my sets of three, say, suppose I started with one, two, three, then the next one was two, three, four, you see I'd overlapped two. I'd defeat myself right away. So instead of messing around with trial and error, the simplest way to solve this is to go one, two, and skip three. So if I do that I'll have this triangle.

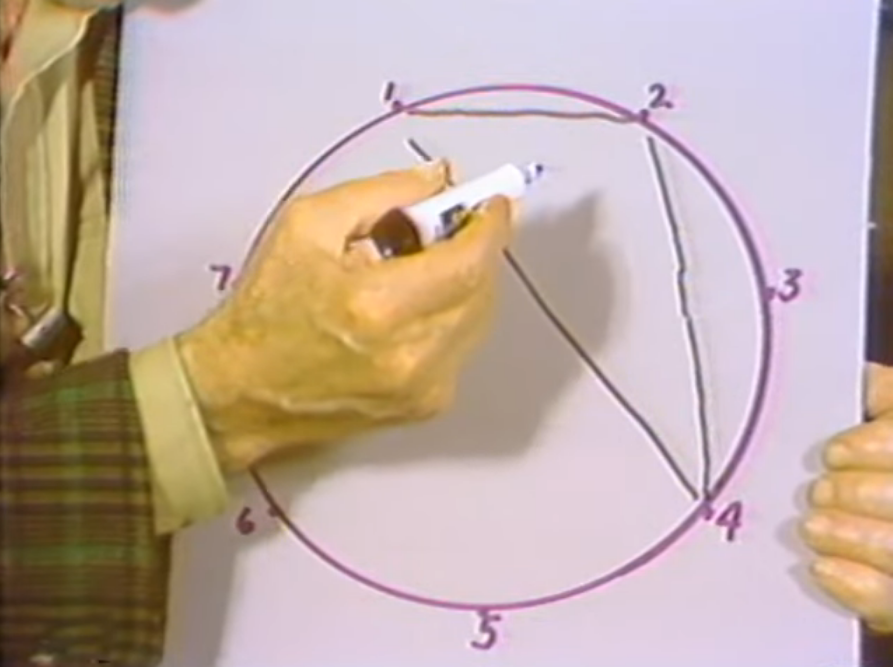
Then the next one I'll go two, three, and skip to five. Now you see I've complied with my rule, because there's no two members in two triangles. As I go along this will get more complicated. The next step is that one here. I've already now got three on top of each other so I'll have to make some way of distinguishing. I'll leave this one white and then this one cross it this way. Now you see this dotted one is covering the striped one and both are under the white one.

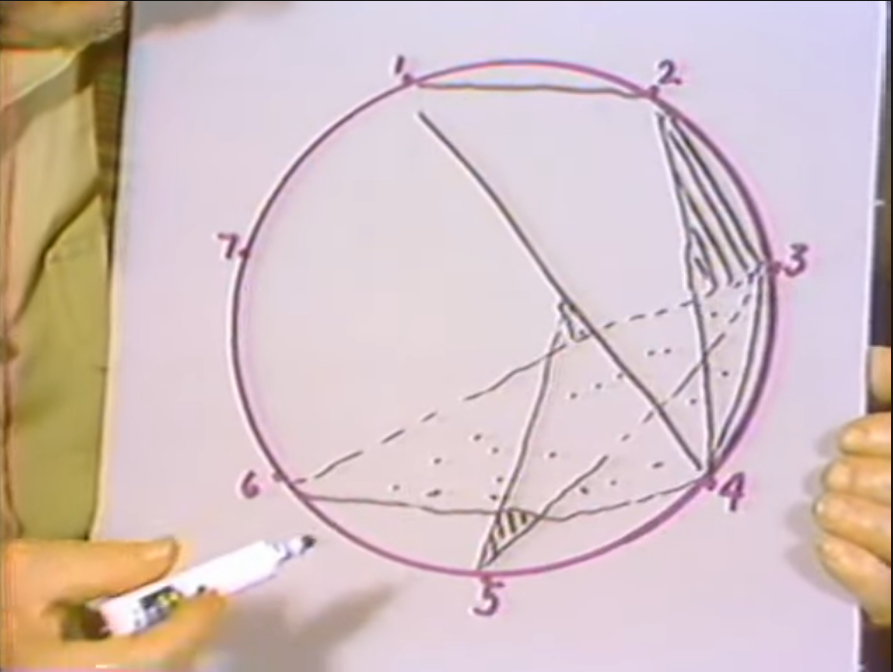
I should have left those out there but anyway bear with me. Next one will be four, five, seven, and the next one five, six, one. The next one, six, seven, two. I've only got one left: seven, six, three. I really should do this under everything but I'll make it very clear that I've now got seven triangles such that no two triangles share two points.

That is another version of the figure that would follow this one. You can see how complicated it would be. I would really have to put in, see, have I joined every point to every other point? Yes I have. I've joined every point every other point, so I've complied with the rule here, and I did it in an orderly fashion, so that you can see that I did it the right way.

Now I began to be curious since there is -- one always expects when you find something mathematical that to be something in reality corresponding to the mathematics -- and of course vice versa -- but in this case of course was setting up a correlation between the seven colors. These seven colors, I mean the coloring problem here -- those seven colors were the seven grand stages of process. But here's something else. This is the committees. These are interrelationships of three of these points, or three of the powers, and they should mean something.

I kept scratching my head about what these committees could mean. I could see no way of correlating them to anything I knew about, and then I remembered the thing I did before. I better just remind you of what it is quickly. I didn't prepare the chart. I took the circle and showed these three triangles, the three types of evolution.

This is the Darwinian evolution, the DNA. This is from attraction, through trial and error to the goal, which is instinct. This is intelligent, seeing how the law works, recognizing what it is, light recognition, recognition of the principle and its characteristic of true thinking, thinking in the better sense of recognizing truth.

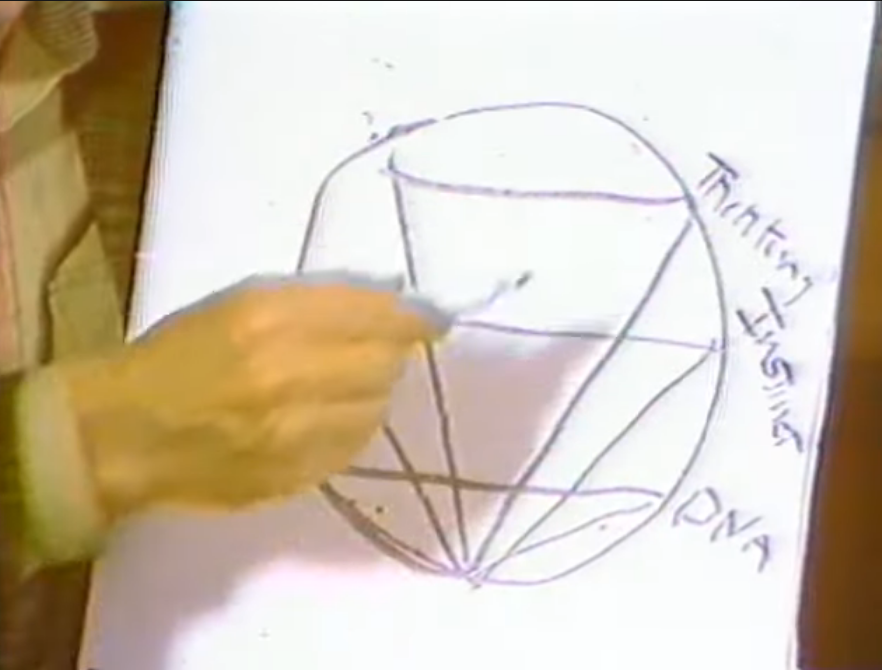
Well I had done that separately, without realizing, or it didn't occur to me that these these are the triangles that were involved in this complicated picture. I could then assign three of them, but how would I assign the rest of them? That didn't come about until I realized that I was neglecting an important rule of process which was that the whole thing is cumulative. It begins simply and then it accumulates this and this this this this. It builds on itself. It's cumulative, so that what I should do is make triangles as I go along. And if I think of starting with one, then I can't have any triangle because there's only one point, nor can I have anything with two. It's not until I get a three that I can create a triangle.

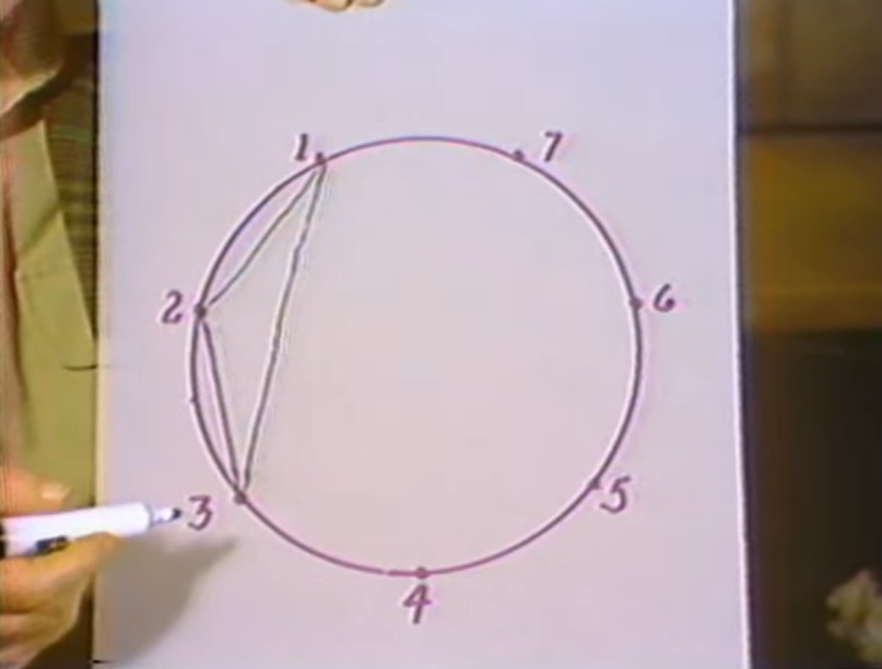
That becomes my first triangle which could be the principle of identity that I referred to as emerging at the third stage.

Now when I come to four I can't make a new triangle because I'll include this whole side and that's against the rule. So it's not until five that I can get another triangle. Then I get the one that corresponded to DNA, in other words, the idea here, and the survival of the fittest, and the good idea, becomes the prototype and evolves the DNA for the species. That was the DNA triangle. Well then when I go to six, let me see if there's another triangle that I can draw from five. I don't think there is. (I'm forgetting my own rules now.) No, it's not until the sixth that I can now draw the triangle that corresponded to instinct, which was this one, from attraction, trial and error to instinct.

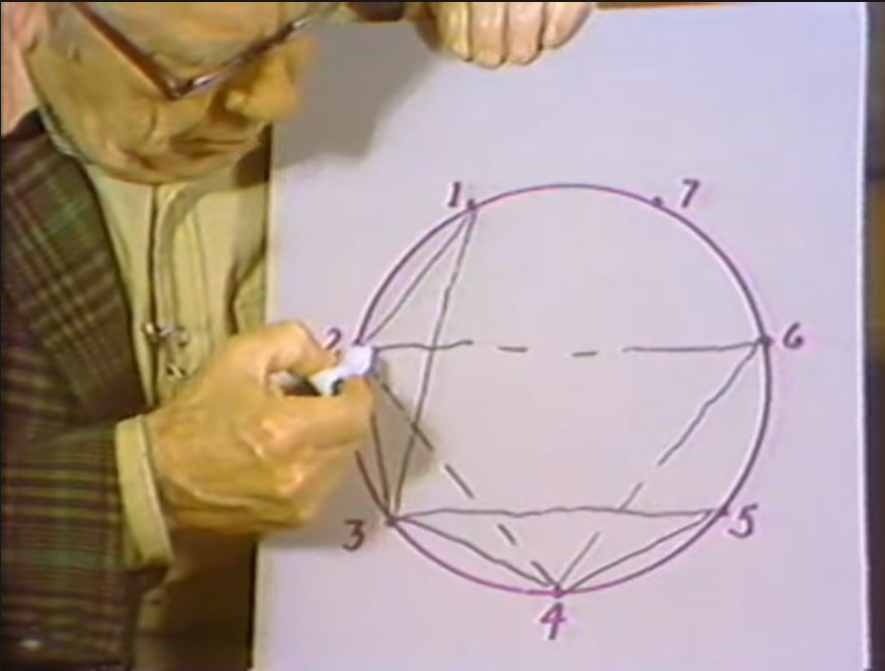
But I can also draw now a new triangle that I didn't have before. That's this one, five, six, and one. So I've got one, two, three, four, triangles at six points.

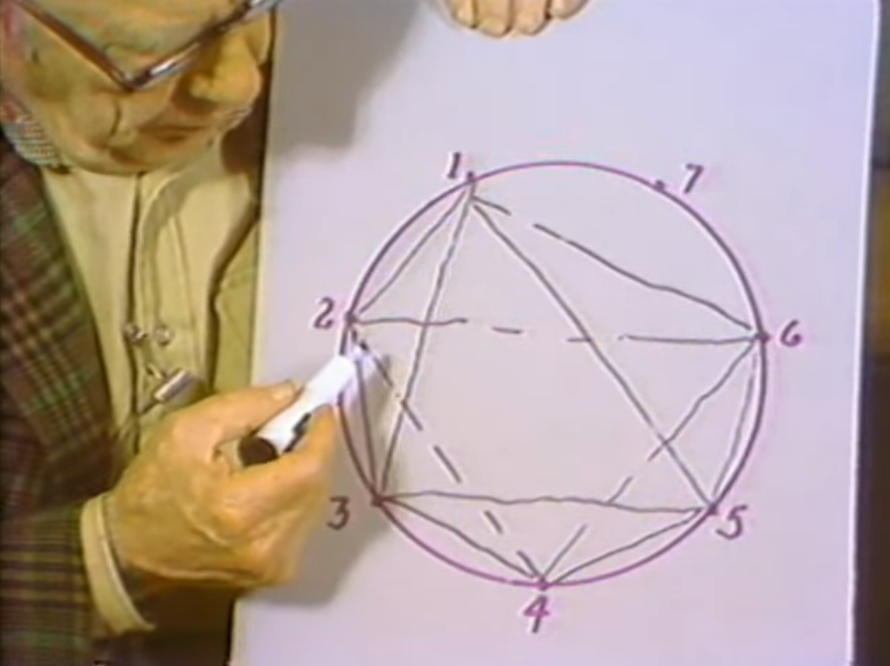
When I come to seven of course I have the one that represents human evolution. The recognizing the law. That's one more. Then I can join this and this and carry that... (I want to be sure to do this right, because it's my last chance... I think it's this way and the other one is this way.) Now see I've added three at the seventh stage, three added up to here. I had four but the four I had plus the three gives me the seven triangles, seven committees, and these would be powers.

Now I'm really trying to talk about the abstract mathematics so I don't have to say what these things mean. In fact I don't even know what these last two triangles mean. But I can account for the rest of them.

First one gives the identity then there are three that give the three types of evolution. And this one that was introduced by five must be the element of choice that comes in with animals because I mean the one that began with six. That was this one, see it goes back to one. One is choice. So it adds choice to what the plant had before. Now that makes the only two unaccounted for are this seven-six-three, which I think is the motivation of structures, or purposeful use of illusion through forms, which would correspond to art. And this possibly is connecting the principle of organization with the raw energy organizing raw energy into machinery that's what another thing that man does.

Now I offer that only tentatively but see what I'm trying to do is is be able to account for more things by the mathematical principles and from the point of view of the present discussion of "Why seven?" it isn't necessary to solve this now. But you see that seven is by far the richest so far because we didn't get any of these triangles until we got to three. Then we didn't add any until we got to five then we got two and we came in with six, we got four, and then jumped three more at seven.

Now if you were to go to eight points you'll find it won't. It breaks down. I think I'll just have to let you try that for yourselves. If you try, if I had eight points, it would break up into two sets. I couldn't follow this rule that every one of these points is related to every other point. Any two triangles share one member. That's one of the rules.

These are all spelled out in the back part of The Reflexive Universe.

Now this really is one of the most powerful reasons of all for the seven, because if the universe was built on an eightfold principle it would split up. If it was built on a six-fold principle it wouldn't be possible to have the richness of interrelationship that the sevenfold makes possible. And the same way for simpler numbers.

So I think that is about about the most powerful. Unfortunately it's quite complicated but it's very interesting. Of course, you could say "Well it's all very simple if the fourness is valid then it takes seven steps to go down and back through the four," but I don't know that that's as convincing. It's not complicated enough to be convincing.

There's one further one that I had never allowed myself because it just seemed too simple, which is this thing that everybody's done when you first start playing with a compass. You found that you can exactly lay out six equal circles around one and that in turn creates a larger circle and you can have six of those around one and and so on ad infinitum.

It's a way of saying as above so below because whatever is true in this larger is true in the smaller. I would draw six circles inside this and a seventh in the center and then each of those would have six and a seventh and so on add infinitum. This is I think a, well the reason I rejected this idea at first was that I'm drawing this on a surface, whereas we want to think about what's going on in at least three dimensions, maybe seven dimensions, who knows. Maybe this kind of thing doesn't go on in seven dimensions.

Well then I realized and it took me a long time to get through this point that no matter how many dimensions you have, a surface is a surface, and this is a property of surfaces. The seven distinctions are, in a non-pejorative sense, superficial. You can write down these distinctions but that's not the same as living through them. But in spite of myself I have to make a map on a two-dimensional surface. And that's really what a surface means: it's the superficial approach. I'm not using it in a, as I said, not in a pejorative sense. It's just that this is the mapping and this is the cost you pay for mapping. It's not the same as experiencing the thing in depth.

Well there's one more principle that I've left out which in a way is the most intriguing but it's also a little more difficult. Can we shoot this tetrahedron again?

Notice that around each vertex there are three triangles. Okay we move to this one. Around each vertex there are now four triangles.

Now this one doesn't show it but if I remember that the internal diagonal is there, there are actually five triangles coming from each point.

See I can count the four on the outside, but if I were to really lay it out there would be not four but five, because of this internal one. Now here you can almost tell by sort of implication that there are going to be six triangles around each point.

You see it's implied by this diagram of circles because if I drew points like that, you see, that would be a triangle and there'd be six of them. Now since six fills up the 180 degrees each triangle has a 60 degrees subtended angle and it's between sides so 6 times 60 is 360. I filled up the circle. I've filled up the plane. I can't add any more triangles even to these hyperdimensional figures which I can't illustrate in three dimensions, because the surface would still contain only 360 degrees regardless of how many dimensions it was in.

Now that says -- it's another way of saying -- you can't go beyond seven, because the six around the one makes seven. It also has a very delightful -- or mind-blowing or something to think about -- feature that, suppose you were making models, you might start out with this simple physical model and this wouldn't have to be a tetrahedron but anything I made out of solid objects would be a model using that dimensionality.

Anything I made out of living objects would be this kind of dimensionality involving, as I said, four triangles around the point. Anything I made out of this, which is the transformation model, would be five points around an apex.

When I get to here, my model has extended to an infinite plane. It's an infinite plane and yet it's not infinite because outside of these circles are more circles going on forever. But this circle is duplicated somewhere else. Each one of these has a duplicate over and over, but such that it's separated from all the others, so that you wouldn't get them mixed up.

This is another reference to the as above so below. Whatever the process is, there are seven stages, just as we found with the ark. The substages and sometimes even sub-sub-stages.

Well okay. Now we're ready for the blockbuster. Having made this model, you wouldn't know whether you were inside the model or outside the model because the thing is perfectly flat. In other words if you could make this model it would be a new universe and I think that's a good place to stop.