|
While reading John Baez's article on octonions, I came upon the illustration of the Fano plane familiar to anyone who has studied octonions for at least 60 seconds. I've seen it many times before and pondered again at what riddles remain buried in its symmetrical shape. 
Then as the article continued, I saw something I hadn't seen before: The Fano... cube? It's another way of rendering the same points. And an insightful one, too. 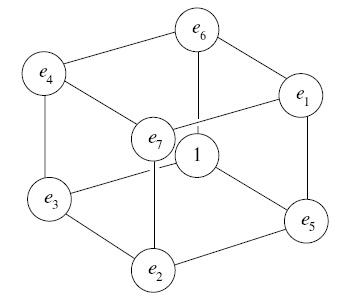
I don't know if it has a name, but as I looked at it, pondering the same riddles as before, I was looking at the various symmetries... and I noticed an asymmetry. I've highlighted it below. I was trying to study the relationships between numbers across the faces of the cube, and I noticed that most of the sequential numbers made diagonal lines across the face or center of the cube... except a couple. Take a look: 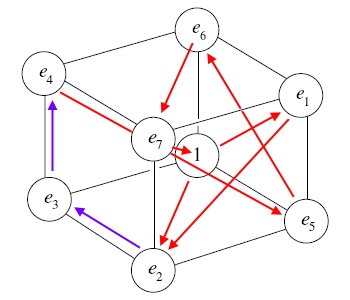
See how most of the lines, the ones colored in red, are going across diagonal spaces? But the two purple lines are orthogonal, not diagonal. Why is this? I honestly don't know enough about the Fano plane to have an answer. I'm just looking at the obvious symmetry/asymmetry, as an artist would, not as a mathematician woul... wait, this is the way mathematicians think, also. Symmetry is a superimportant component in the study of math and physics. So I studied the patterns a little more closely, and soon realized that by moving a few corners around, the asymmetry could be made symmetrical. I can only hold a couple free variables in my head at once, so I couldn't tell if it worked all the way through. I needed to visualize the changes more carefully. I opened up Paint.Net and tweaked the image a little, til I came up with this: 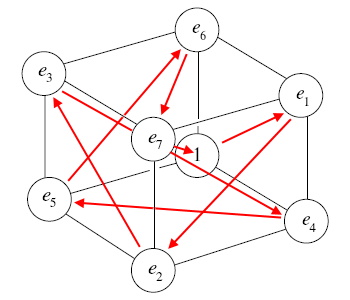
Now all the red lines cross diagonally. I have no idea if this changes anything mathematically at all, or if it is merely a cosmetic change. This is just a thing my mind does when looking at complex, beautiful patterns. Having gotten a well-behaved cube, I went back to the familiar Fano plane diagram and tweaked it according to the changes I had made with the cube. Here is a little note I wrote to keep track of the changes, because I was having a hard time moving three variables simultaneously in my head:
As you can see in the resulting illustration below, all this is simply rotating the position of 3, 4, and 5. The other vertexes remain the same. 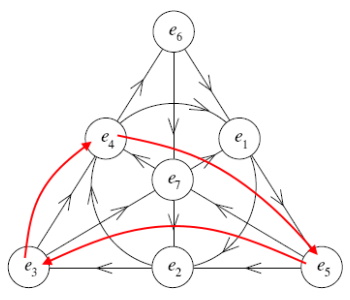
With the new change, the directions of the arrows (which indicate the order of operations allowed) changes for a single line (or dual, depending on how you count), the line from e3-e7-e4. 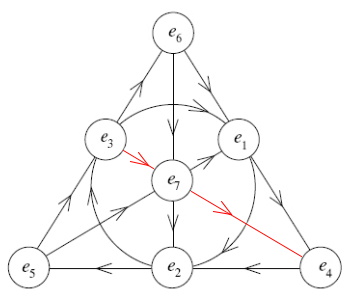
The nice thing about this arrangement is that e1-e2-e3 are now pleasantly arranged around the circle, before jumping across the e7 in the center to the e4 in the bottom right corner. Then, the "spiral" continues, from e4-e5-e6, before returning to the e7 in the center. As this happens to more closely match a thought experiment I've studied for years, I prefer this arrangement. I guess I should study what's happening under the hood now that I've replaced the hood. Here is the completed, new Fano Plane Transmogrified, nicely framed, for putting on your wall: 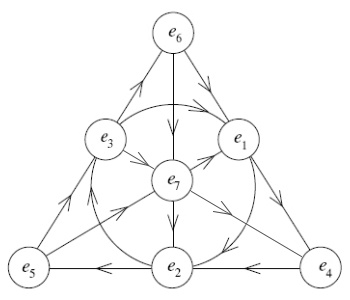
Fano Plane Transmogrified
Feel free to download the image and use it, if you want. If anyone reading this can comment on whether this affects our understanding of octonions or not, please let me know. Otherwise, I'll eventually spend the time to figure this out, but for now I have other work I must get to. But before I go, the last line of this particular page in Baez's article answers another thought experiment I've contemplated: Is there a way to make octonions associative and commutative? (I'm pretty certain I've found a way to make quaternions commutative, so this is an obvious next step.) Apparently there is. Baez writes: "In this symmetric monoidal category, the octonions are a commutative monoid object. In less technical terms: this category provides a context in which the octonions are commutative and associative! So far this idea has just begun to be exploited." Searching to find more on this idea turned up some more math that's over my head... but then this, which looks to be a great introduction to monoids in category theory in an intuitive, playful, way, which may give me a toe-hold into category theory. In the past, I've studied category theory (and its cozy relationship to set theory which I already know is flawed, or, rather, I should say, not ontologically deep enough to be the foundation of math) enough to know that it's not "the answer" that some claim it to be -- my own ideas go one step deeper in the ontology of math because they talk about the nature of division in a way I've yet to see elsewhere -- but not yet enough to know how it works in detail. So I'm curious about the details of category theory. I'm okay with pictures of dinosaurs and the story of evolution being used to teach the concepts. All I need is a toe-hold, but attempts thus far have only given me vague outlines of ideas because I haven't been able to latch onto the concepts intuitively. "If there is one structure that permeates category theory and, by implication, the whole of mathematics, it’s the monoid. To study the evolution of this concept is to study the power of abstraction and the idea of getting more for less, which is at the core of mathematics. When I say “evolution” I don’t necessarily mean chronological development. I’m looking at a monoid as if it were a life form evolving through various eons of abstraction." -- Bartosz Milewski Sounds great. I bolded the part that catches my eye. People who stick with chronological development of a mathematical idea are stuck in a linear way of understanding things that often makes it more difficult to understand. If this article by Bartosz Milewski is any good, I'm sure I'll be posting related thoughts on my own website soon enough. UpdateA couple weeks later (Feb 15, 2022), I found this mention of the same diagram from Baez, in an article called The Fano Plane Revisualized: Baez's statement that "lines in the Fano plane correspond to planes through the origin [the vertex labeled '1'] in this cube" might be taken literally by some viewers of the Baez slides, with the planes regarded as cutting a cube in Euclidean 3-space. So interpreted, the statement would be false. But this is not what he meant. Ah good. I didn't imagine it as a cube, I understood that it was a diagram, not a literal cube. However, I now wonder if imagining it as a tetrahedron, as I do in my next post, is also prohibited. |
|||||||