The word infinite is from the Latin roots for "un-limited" or another way to say it: "without-end." Structurally, this word is similar to Greek a-perion, Hebrew ein-sof, Chinese tai-ji, and many others, all referring to the same underlying concept: that which is so great it is beyond ability to measure, endless. (Like un-measureable, "endless" is of course another example of the same "negate something-limited" structure, which combines into one word a negative with an ultimate limit of some kind.)
It's one of those little things most people don't notice or care about, but I believe there is actually a really deep question going right to the heart of the way we perceive what we call reality on a fundamental level:
Why is a concept which is the utmost, the greatest, the ultimate, the infinite, the "beyond-measure," consistently defined by reference to what it is not, rather than by what it is, no matter what language you choose?
I recently faced this paradoxical question directly when I was working on a thought experiment which took the two endpoints of positive and negative infinity, brought them together, and merged them with zero where it lives at the midpoint of the number line (I turned the ordinary number line into a circle). That may sound like a peculiar idea at first, but it's a thought experiment I have entertained numerous times over the past decade or more because doing so answers a number of other questions.
This particular thought experiment reveals hidden insights about fundamental math and logic structures, often hidden because we take our foundation for granted and don't dig deeper in some of its riddles. Hence I was contemplating this idea the other day when some missing pieces involving complex numbers and the Riemann Sphere fell into place. Suddenly, before my eyes for the first time ever, was a coherent visual representation drawing on multiple separate thought experiments coming together into a single intuitively simple form.
A coherent way to visualize the union of several paradoxes
Here is a preliminary image I created while writing about this insight the other day. It's the well-known Riemann Sphere rotated 90 degrees backward so that Infinity (which is usually at the top) is at the backside. This rotation also brings the bottom Zero to the front (and also perceptually nearer to the ∞ than I'd ever seen it before, which is important. That small shift in perspective may have been the trigger for what happened next.) To do the thought experiment, I started with this image from Wikipedia and brought the ∞ and the 0 together into the center where the question mark is pointing (see illustration):
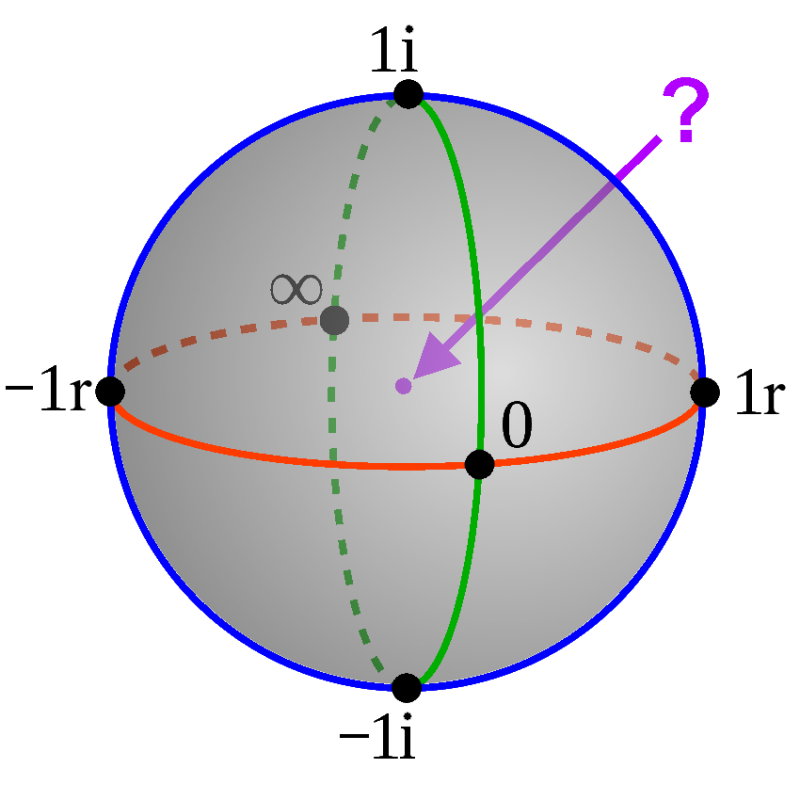
For the first time, probably because I was using a sphere instead of a linear number line, it all worked! Not only could ∞ and 0 coherently unite at the center, but doing this move left two smaller question marks: What goes in the places where ∞ and 0 were (i.e. where they can be seen in the image above)? I thought about this for a while, but it didn't take long to see there was now room for complex "j" and "k" to fall neatly into place where the ∞ and the 0 had been, without disrupting anything else. I confess I'm not smart enough to know why this shouldn't work, so I continued with the thought experiment since it seemed to fit and was getting profound. I continued making similar sketches using Paint.Net to quickly draft the ideas, and eventually developed things to the point where I wanted a new name for the point at the center where ∞ and 0 are combined.
Searching for an apt name, I experimented with numerous options over several days, whenever I had an idle moment. I began researching things like the word coined by ancient Greek Anaximander: aperion, and its predecessor, the word arché, said to be coined by his predecessor Thales (see illustration). I began looking into the concept of infinity in other languages, as well as looking at different possible symbols. At one point, I drew a symbol which combined zero and the lemniscate ∞ into a single shape.
As symbols go, it's a pretty one which conveys its meaning quickly, in spite of looking like something from a Prince album cover. I especially liked the fact that this new symbol for infinity had three parts instead of the usual two, which corresponded well with my understanding of infinity as it is perceived using ternary logic. Many is the time I've pointed out that the main exclusion of binary logic's "excluded middle" is infinity itself. Likewise, I have lamented the resulting hard link between binary logic and finity.
However, much though I liked the new zerofinity symbol, I did not like the resulting complexity of the symbol -- its shape ought be more simple, more elegant, to convey the essential simplicity, or singularitiness, in this new kind of infinity. I also knew that one of the fundamental stumbling-blocks to understanding ternary logic in its own terms is the tendency to think that ternary "three" is simply "one" plus "two." The true ternary "three" arises in a non-linear manner, not simply serially after "two." Therefore merging a lemniscate symbol with a zero might be a nice way to begin, but the stumbling-block of linearity would be right there in front of everyone, so I sought something deeper and more intrinsically elegant.
Infinity in different languages leads to what is infinity?
Working on etymologies and intrinsic rules like this, about then I noticed that I kept encountering references to infinity in different ancient languages, but they were all structurally similar: they all could be translated to something very close to "without-end." Yet they were also all talking about something enormous, vast, encompassing, boundless, so immense as to contain everything everywhere. As I thought about this, it seemed obvious that some unknown perceptual dynamic had led humans to repeatedly arrive at a word for immeasureable which was rooted in the measureable. I began to wonder, how many cultures defined infinity by saying what it is not? And why not call it what it is, instead of what it is not?
This led to the question: if we're going to go that direction, what is it? What is infinity, really?
Thought experiments in this direction were fruitful right away. For years, I've been studying the history of a curious phrase: "God is an infinite sphere, the center of which is everywhere, the circumference nowhere." I well know the infinite is not simply "out-there," "far-away," "at-the-end-of-the-numbers," "beyond-all-that-is," but it is right here -- and everywhere else also. Everywhere in space, everywhere in time, everywhere in all dimensions. It is true that what we call infinite has several branches of meaning (like "potential" vs. "actual" and "qualitative" vs. "quantitative", "countable" vs. "uncountable," etc.), but the trunk of its meaning is consistently a reference to something endlessly unbounded.
If infinity is so unbounded at its root essence, then why does it have boundaries? Why does it stop at the end of mathematics? Why can it not penetrate everything everywhere always? Suffice it to say that I have long thought confining infinity to a limited place in mathematics -- at the end of countable numbers -- reveals a weak understanding of how truly vast "endless" infinity actually is.
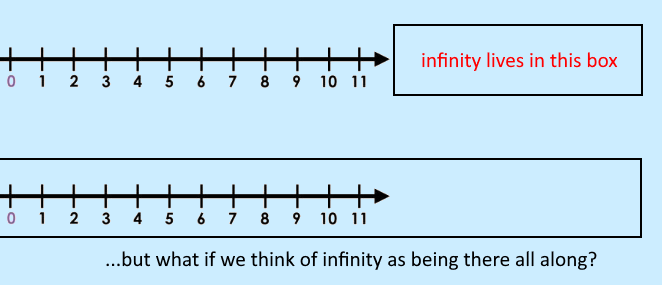In short, I well understand that infinity exists not only "after" all countable numbers but it also penetrates all of them from beginning to end -- although I will admit that I only realized the clarity of that thought just now as I wrote it. I promptly bolded it because it is clear and succinct. Here, I made an image to convey the idea (see illustration):
If Georg Cantor's ideas on infinity "created a paradise" in the words of the great mathematician David Hilbert, what describes the beyond-paradisaical beauty of the significantly larger form of "infinity" -- the largest possible -- which encompasses all of Cantor's paradise, plus all the rest of mathematics, plus all of physics as well? (For a visualization of what I mean, consider the illustration above. Instead of one of the black-bordered boxes containing infinity, how about the whole illustration, or better still, how about this whole article? The whole Internet? Where do we stop measuring infinity?)
If we're going to call something "without-end" then why are we giving it an end? Is the "set" of mathematical Set Theory not itself contained within the greater infinity which is the set of real, physical, life itself? What exactly forbids mathematics from touching physics... forever... even at the outermost periphery of infinity which supposedly goes on forever? Clearly it doesn't go on forever if it is limited to the boundaries of mathematics.
This true "deep infinity" so utterly dwarfs the already-stupendous mathematical infinities of Cantor's paradise, there is most certainly a need for a new word describing it which is not built out of a reference to what it is not, pardon the double-negative. An "endless" infinity which "ends" and is defined by what it is not is just as paradoxical as Euclid's "a point is that which has no part," which I have discovered in other thought experiments is ironically the founding-stone that inevitably leads to this paradox with infinity.
We need something new, built from the ground-up with an etymological reference to its everywhereness
I began researching this concept. Soon I was reading about Ein Sof (again), I was reading about Ayin and Yesh (that was a new one). Then I was back to apeiron and Anaximander, then over to Aristotle, and forward again to Hilbert and Einstein, then back to (yet another) PDF on the history of infinity in case I might find something new.
I've read a dozen of these kinds of PDFs over the years because the history of infinity is equally as fascinating as the history of zero, both of which have met fierce resistance within mathematics but are accepted as fundamental elements these days which even the youngest schoolchildren learn. In fact, while randomly at a bookstore two days ago, I of course bought one thing: a book on infinity, ironically titled "Beyond Infinity" as if there could be something beyond that which is endless (see illustration). Maybe we gravitate to such "beyond beyond-end" metaphors because we sense that infinity is not yet "the ultimate" which it pretends?
I was up in the middle of the night, learning that Tai Chi was not just an elegant form of boxing but a philosophical concept "tai-ji" meaning something akin to "Supreme Beyond-Pole," which is not quite the same as the "Supreme Ultimate" I learned back when I took a semester of Tai Chi years ago. My mind wandered often to resolving this quandary for several days.
I found myself in a curious research paper reading about the structure of what happens beneath Planck scale, where physics breaks down and intuitively everything becomes one with everything but nobody talks about it because they think the Planck measure, at 10-35 meters, is as small as anything can ever be.
Coincidentally, that particular research paper was due to another line of study which fell into my lap at the same time I was researching infinity. Such coincidences happen often when I am studying math, so much that they should not be called coincidences, but synchronicities. Confirmation that it was a synchronicity came from a rather literally random direction that I should briefly explain.
Brief detour to breakdown a synchronicity
Long ago, while studying similar ideas, I was meditating, and pretty far away from rational thought (see illustration) when I gained the purely intuitive (i.e. non-rational) understanding that true Infinity, true Oneness, and true Random -- all three of these -- were somehow the same thing. I made a note to myself during that meditative thought experiment, telling a future me in the strongest possible way: "Infinity, Oneness and Random are all the same. Remember that!"
Without going into more detail on a decidedly non-linear hard-to-explain process, I'll simply say that is why I went to the search engines looking for a symbol for random. To me, random is somehow related to infinity, so I cannot pursue one for long without bringing in the other. Hopefully one day, I'll find the more rational version of this insight so I can share it with others.
However, there is no reliable symbol for random.
Honest, try and search, you'll find fragments, some proposed ideas (card shuffling, dice-rolling, etc.) which are appropriate to specific contexts, and lots of debate, but nothing definitive like you find with Infinity or One or Zero, these kinds of big ideas. Random is a hard idea to symbolize, so... it remains to be symbolized.
I dug deeper. And that's where I first came across the Greek letter "ξ" pronounced "xsi," which Riemann used when writing about a variation of his famous zeta function (later the uppercase form of xsi "Ξ" was adopted for this purpose). According to Wikipedia, it's also a symbol used when talking about random variables, which is why it came up in my search.
I pondered the simplicity, elegance, and beauty of that symbol, thinking about its three curliques, which brought me back to ternary logic and how its "third pole" gently blends everything into infinity... and then remembered I was on the larger task of finding a symbol and name for Infinity and Oneness, not Random. No one would get this reference to random but me. So I dropped it, and continued the larger search.
Looking at Greek and Latin roots, I found myself back in Strong's concordance again, contemplating the meaning of the word arché, not because of its relationship with infinity, but this time because "beginning" is the opposite of "end" in the "without-end" of "infinity."
Arché means "beginning" and "origin" and even "sovereign authority," and it has the benefit of being the word that Thales used... long ago... when the idea of infinity was just beginning to be understood. Clearly, arché has a solid etymological root with which to begin.
Okay, the Greek root for "beginning" is going to work, so how about considering a structural opposite to "without-end" by looking at the etymology of "with"? A search engine quickly pulled up a list of Greek and Latin prefixes. I went to Latin first, but "com-arché" or "coarché" or "co-initio" didn't feel right. I went to the Greek roots for the prefix "with."
Syn. That's the Greek root. As I searched around a little more, it was becoming clear that for what I was seeking, "synarché" would be the most accurate neologism. But happily, this time when I went to Strong's concordance for another look at arché, my search engine delivered a webpage that included a reference to Thayer's Greek Lexicon, and there it was (see illustration):
There is an older form of "syn" and it begins with the wonderful ξ! The word is "ξύν," pronounced "ksun" or "xsin." Excited to see the xsi again, I joined the two roots: xsinarché, then ksunarché, but alas, if I wanted anyone else to understand what I was saying, xsinarché was obscure, worse than the awkwardness of cominitio by a yard.
I thought for a little while about that. Wait, what about using the transliteration synarché, but still refering to the original root ξύν xsun when using the Greek?
And there you have it. The origin of "with-beginning" or synarché, spelled with a ξ. Etymologically sound, graphically elegant, a nice solid foundation upon which to build a truly paradisaical "infinity."
Now the important step of making it easier for others to use
With that solved, there remained the issue of whether to call this synarché or synarche, to make it easier for others to write it. Diacriticals like é are not always easy to enter into a computer, say, for example, in a URL. Or they can cause display problems in some older terminals (which display something like "synarché"). Should it be www.synarché.org or www.synarche.org? One should think about such consequences when one creates new words. And what about mathematicians who are already using xsi to refer to random variables? Are there other similar collisions? (Yes, for one example, a little bit of research on the similar word synarchy turns up a whole host of references that are not at all related to mathematical symbols for infinity.)
The answer will not please everyone, but there may not be a way to please everyone on such matters -- the experts who are to be pleased are often the most hair-splitting, since it is by splitting hairs that etymological experts learn what they know. So here's the answer:
The point where mathematical infinity touches reality
Synarché, a new word for what was formerly known as infinity -- well, actually, something much bigger -- can be spelled synarché or synarche; either one is acceptable, but synarchy is already taken, so we'll hold firm to the e at the end to keep things clear. The symbol xsi "ξ", which is to be used when referring to the center of the rotated Riemann Sphere with i, j, and k as described above, or to the point where mathematical infinity touches reality, or to all of creation, is just too beautiful to lay aside in pursuit of something more pedantically perfect.
If my intuition about it is correct, people who are already using xsi "ξ" for random variables may enjoy the fact that they're also touching infinity from time to time as they go about their work. (I have a future essay in mind regarding specifically what is meant by "touching infinity," or rather, we should now say "touching synarché," since mathematical infinity cannot be touched, but synarché can -- it is everywhere.) If I am incorrect, no one will care about what I write here so the point is moot.
My appeal is to mathematical beauty, and I hope, as I continue researching this delightful discovery, it continues to astonish and inspire, and ultimately, it works.
Some caveats
I've been gloriously wrong before. Many have stood at the high precipice of defining a new concept within mathematics and discovered that they were wrong. Perhaps as many more never did figure out that they were wrong... but they were. Thus, I may be wrong, and hopefully I have the ability to walk down from a precipice of wrongness if need be. In which case, this is a fun adventure which will soon be forgotten, and nothing of consequence has happened.
For those who appreciate this idea but prefer to stay out of theological debates, the threefold vortex of lowercase xsi refers to "Infinity, Oneness, and Random," or, if that's still too far out there, it refers to the graceful blending-into-infinity nature of the third pole of ternary logic, or even simply the original approach of joining a lemniscate ∞ with a zero 0.
Last thing; a curious puzzle: as a letter, the original meaning of Xsi is "detached from" which is what the three dashes in the uppercase version "Ξ" represent -- the middle bar is detached from what is above and below. It's curious because the full prefix "ksun" or "syn" (ξύν) itself means "with."
