The other day, I was tweaking the symmetry of the Fano plane, as described in a previous post, and ended the experiment by pondering whether there was more to the idea than I could see. A few days passed, and then today, while I was reading a completely unrelated description of energy flowing into a tetrahedral shape, I noticed that the diagrams were making a similar pattern to the symmetry I had recently discovered. I compared the two concepts, and lo and behold, discovered that the symmetrical Fano plane/octonion cube aligns quite nicely with a tetrahedron.
Here is what I had previously discovered:
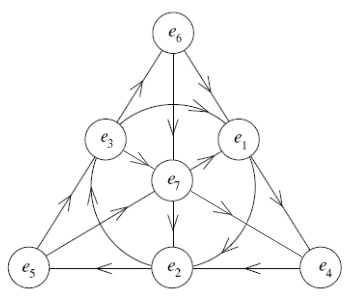
If you read the previous article, you know I got to that more elegant symmetry by taking the hint from the cube in John Baez's article on octonions. Here's my version of his cube:
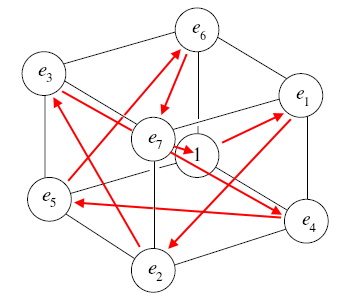
Now compare it with this, which I just discovered today (I made this image using Paint.Net):
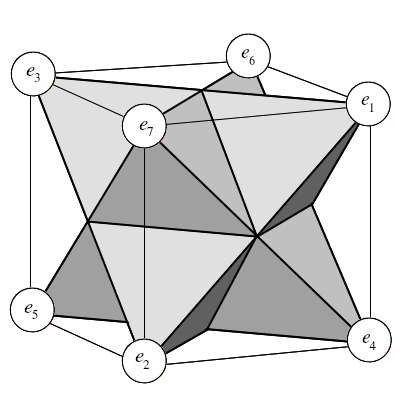
Trace with your finger the movement from 1 to 2, 2 to 3, 3 to 4, etc. It's elegant. Note the origin is the only point of the 8 which is hidden, in the back right corner.
As the article I'm reading later goes into a related symmetry of nine points (a cube is a symmetry of eight points), it seems natural for me to consider that there may be another point hidden in the middle of this cube, like so:
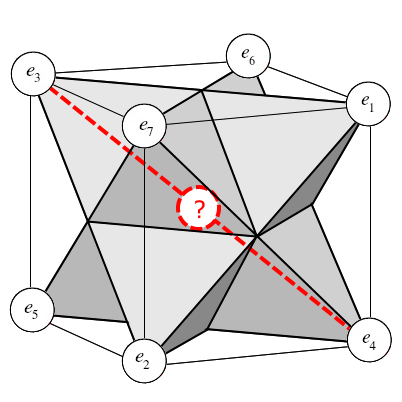
Although I only highlighted the line from 3 to 4, this center point gets crossed twice, if you follow the energy flow concept.
Searching online, it is clear that I'm not the first to notice the relationship between Fano and tetrahedrons:
https://commons.wikimedia.org/wiki/File:Facial_Fano_plane_within_Fano_three-space.
https://www.geogebra.org/m/jejVt8MW
https://en.wikipedia.org/wiki/PG(3,2)
http://m759.net/wordpress/?p=46338
http://www.log24.com/log/pix14C/141129-Polster-Fano-Tetrahedron.jpg
Again, I have little time to dig into this at the moment, but here it is for you to think about.